题目内容
已知1+x+x2+x3=0，求x+x2+x3+…+x2004的值．
考点：因式分解的应用
专题：
分析：观察整式x+x2+x3+…+x2004通过提取公因式，可分解为含有因式1+x+x2+x3的形式．再将1+x+x2+x3的值作为一个整体代入求解．
解答：解：∵1+x+x2+x3=0，
∴x+x2+x3+…+x2004
=x（1+x+x2+x3）+x5（1+x+x2+x3）+x9（1+x+x2+x3）+…+x1997（1+x+x2+x3）+x2001（1+x+x2+x3）
=（1+x+x2+x3）（x+x5+x9+x12+…+x1997+x2001）
=0．
∴x+x2+x3+…+x2004
=x（1+x+x2+x3）+x5（1+x+x2+x3）+x9（1+x+x2+x3）+…+x1997（1+x+x2+x3）+x2001（1+x+x2+x3）
=（1+x+x2+x3）（x+x5+x9+x12+…+x1997+x2001）
=0．
点评：本题考查了因式分解，解决本题的关键是对x+x2+x3+…+x2004分解成为含有因式1+x+x2+x3的形式．
练习册系列答案
相关题目
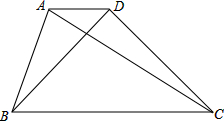如图，已知梯形ABCD中，AD∥CB，AD=1，BC=4，BD=3，AC=4，求梯形ABCD面积．
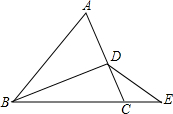已知在△ABC中，D点在AC上，E点在BC的延长线上，求证：∠ADB=∠CBD+∠CDE+∠E．
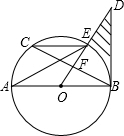如图，已知AB是⊙O的直径，点E是弧BC的中点，DE与BC交于点F，∠CEA=∠ODB．