题目内容
【题目】如图,AD是△ABC的高线,在BC边上截取点E,使得CE=BD,过E作EF∥AB,过C作CP⊥BC交EF于点P。过B作BM⊥AC于M,连接EM、PM。
(1)依题意补全图形;
(2)若AD=DC,探究EM与PM的数量关系与位置关系,并加以证明。

【答案】(1)见解析;(2)EM⊥PM,EM=PM,证明见解析.
【解析】
(1)根据要求画出图形即可;
(2)连接MD,证明△ABD≌△PEC,则AD=PC,可得出PC=DC,再证△DCM≌△PCM,则MD=MP,∠PMC=∠DMC,再证△MDB≌△MEC,则MD=ME,∠BMD=∠CME,即可得出EM与PM的数量关系与位置关系.
解:(1)补全的图形如图所示;
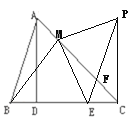
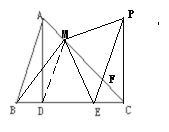
(2)EM⊥PM,EM=PM.
证明:连接DM,∵EF∥AB,∴∠ABD=∠PEC,
∵AD是△ABC的高线,CP⊥BC,
∴∠ADB=∠PCE=90°,
∵BD=EC,
∴△ABD≌△PEC,
∴AD=PC,
∵AD=DC,
∴PC=DC,
∵AD是△ABC的高线,CP⊥BC,AD=DC,
∴∠ACD=∠ACP=45°,
又∵CM=CM,
∴△DCM≌△PCM,
∴MD=MP,∠PMC=∠DMC;
∵BM⊥AC,∠ACD=45°,
∴MB=MC,∠ACD=∠MBC=45°,
又∵BD=CE,
∴△MDB≌△MEC,
∴MD=ME,∠BMD=∠CME,
∴MP=ME;
∵BM⊥AC,
∴∠BMD +∠DMC=90°,
∵∠BMD=∠CME,∠PMC=∠DMC,
∴∠CME +∠PMC =90°,即MP⊥ME,
∴EM与PM的数量关系与位置关系是:EM⊥PM,EM=PM.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目