题目内容
如图，直线AB∥CD，∠1=（3x+10）°，∠2=（5x+10）°．求∠1的度数．
解：∵AB∥CD，∠1=（3x+10）°，∴∠1=∠3=（3x+10）°
又∵∠2+∠3=180°，
∴∠2=（5x+10）°，
∴5x+10+3x+10=180，
解得：x=20，
∴∠1=（3x+10）°=70°．
分析：由直线AB∥CD，根据两直线平行，同位角相等，即可求得∠1=∠3，又由邻补角的定义求得方程5x+10+3x+10=180，解方程即可求得∠1的度数．
点评：此题考查了平行线的性质与邻补角的定义．解题的关键是注意掌握两直线平行，同位角相等定理的应用．
练习册系列答案
相关题目
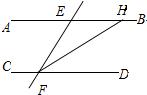22、如图，直线AB∥CD，直线EF分别交直线AB、CD于点E、F，FH平分∠EFD，若∠FEH=110°，求∠EHF的度数．
2、如图，直线AB∥CD，EF⊥AB于E，交CD于F，直线MN交AB于M，CD于N，EF于O，则直线AB和CD之间的距离是哪个线段的长（ ）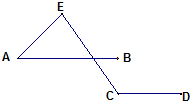
9、如图，直线AB∥CD，∠A=45°，∠C=125°，则∠E=
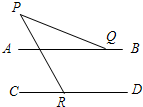14、如图，直线AB∥CD，∠PQA=25°，∠PRC=60°，则∠P=
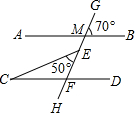（2012•高安市二模）如图，直线AB∥CD，GH与AB、CD分别交于点M、F，若∠GMB=70°，∠CEF=50°，则∠C=