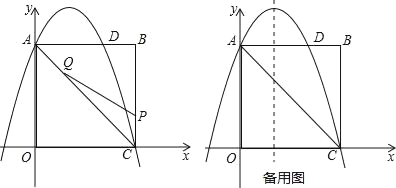
��Ŀ����
����Ŀ����ͼ��ʾ����ABCΪRt������ACB��90�㣬��DΪAB���е㣬��EΪ��AC�ϵĵ㣬����DE������E��EF��ED��BC��F����DE��EFΪ�ڱ�������DEFG����֪AC��8��
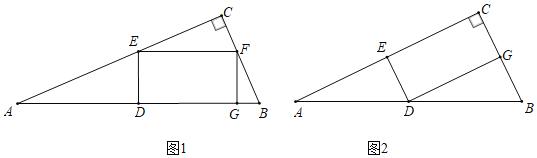
��1����ͼ1��ʾ����BC��6����G�ڱ�AB��ʱ����DE�ij���
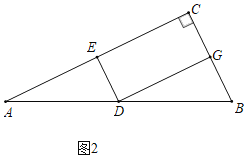
��2����ͼ2��ʾ����![]() ����G�ڱ�BC��ʱ����BC�ij���
����G�ڱ�BC��ʱ����BC�ij���
��3������![]() ���ҵ�Gǡ������Rt��ABC�ı��ϣ���BC�ij���
���ҵ�Gǡ������Rt��ABC�ı��ϣ���BC�ij���
����![]() ��nΪ�����������ҵ�Gǡ������Rt��ABC�ı��ϣ���ֱ��д��BC�ij���
��nΪ�����������ҵ�Gǡ������Rt��ABC�ı��ϣ���ֱ��д��BC�ij���
���𰸡���1��DE��![]() ����2��BC��4����3����BC��2��BC��8
����2��BC��4����3����BC��2��BC��8![]() -16����BC��
-16����BC��![]() ��
��![]() ��
��
��������
��1�����ù�ϵʽtan��A��![]() �����ɽ�����⣮
�����ɽ�����⣮
��2����ͼ2�У���DE��x����EF��EC��2x��֤��AE��EC��BC��2DE���ɽ�����⣮
��3���ٷֵ�G��BC��AB���������ηֱ���⣮�ڽⷨ���Ƣ٣�
��1����ͼ1�У�

��Rt��ABC����AC��8��BC��6��
��AB��![]() ��10��
��10��
��D��AB�е㣬
��AD��DB��5��
�ߡ�A����A��
��tan��A��![]() ��
��
��![]() ��
��
��![]() ��
��
��2����ͼ2�У���DE��x����EF��EC��2x��
��DE��BC��AD��DB��
��AE��EC��2x��
��4x��8��
��x��2��
��DE��![]() BC��
BC��
��BC��2DE��4��
��3���ٵ���G����BC����ʱ����ͼ2�У���DE��x����EF��EC��4x��
�ɵã�AE��EC��4x��8x��8��
��x��1��
��BC��2DE��2��
����G����AB����ʱ��
��DH��AC��H����DH��x����CE��4x��BC��2x��EH��4��4x��
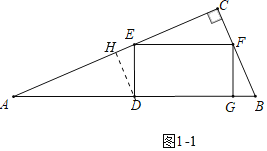
���á�HDE�ס�CAB���ɵ�![]() �����
�����![]() ����
����![]() ��
��
����![]() ��nΪ��������ʱ��ͬ����֪��
��nΪ��������ʱ��ͬ����֪��![]() ��
��![]() ��
��

 ������ϵ�д�
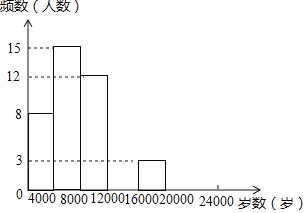
������ϵ�д�����Ŀ���ֽ����˶�����Խ��Խ����˹�ע��ϲ����ij��ȤС���������������50����ʦij�ա����˶����еIJ����������ͳ�����������������µ�ͳ��ͼ��������������
���� | Ƶ�� | Ƶ�� |
0��x��4000 | 8 | a |
4000��x��8000 | 15 | 0.3 |
8000��x��12000 | 12 | b |
12000��x��16000 | c | 0.2 |
16000��x��20000 | 3 | 0.06 |
20000��x��24000 | d | 0.04 |
�����������Ϣ������������⣺
��1��д��a��b��c��d��ֵ����ȫƵ���ֲ�ֱ��ͼ��
��2������Լ��37800����ʦ���õ�����������ݹ��������߲�������12000��������12000�����Ľ�ʦ�ж�������
��3������50��������Ľ�ʦ�У�ѡȡ�����߲�������16000��������16000����������ʦ���ҷ����ĵã���ѡȡ��������ʦǡ�ö���20000��������20000�������ϵĸ��ʣ�