题目内容
【题目】如图，点D是∠AOB的角平分线OC上的任意一点.
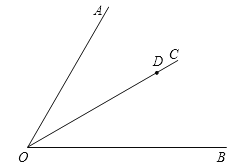
（1）按下列要求画出图形.
①过点D画DE∥OA，DE与OB交于点E；
②过点D画DF⊥OC，垂足为点D，DF与OB交于点F；
③过点D画DG⊥OA，垂足为点G，量得点D到射线OA的距离等于_____mm（精确到1mm）；
（2）在（1）所画出的图形中，若∠AOB=n，则∠EDF=____________度（用含n的代数式表示）.
【答案】（1）①详见解析；②详见解析；③20；（2）(90-
n)
【解析】
（1）根据题中要求作出相应平行线和垂线，然后量出DG的长度；
（2）根据角平分线可得∠AOD＝∠COB=
°，又因为平行可得∠ODE=∠AOD=°，即可得到∠EDF＝(90-
n)°
解：（1）①②③如图1所示；
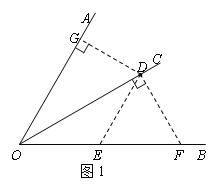
③ 20（允许误差范围20±3）；
（2）∵OC平分∠AOB
∴∠AOD＝∠COB=°
又∵OA∥DE
∴∠ODE=∠AOD=°
∵DF⊥OC
∴∠ODF＝90°
∴∠EDF＝(90-n)°
故答案为 (90-n) .
练习册系列答案
阅读快车系列答案
相关题目
