题目内容
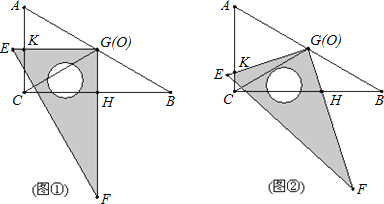
【题目】把两个全等的直角三角板ABC和EFG叠放在一起，使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合，其中∠B＝∠F＝30°，斜边AB和EF长均为4.
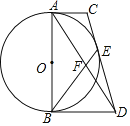
(1)当 EG⊥AC于点K，GF⊥BC于点H时（如图①），求GH：GK的值.
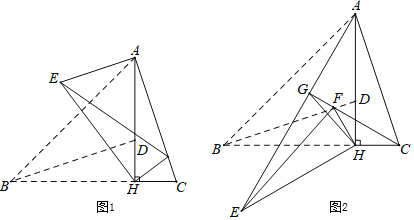
(2) 现将三角板EFG由图①所示的位置绕O点沿逆时针方向旋转，旋转角α满足条件：0°＜α<30°（如图②），EG交AC于点K ，GF交BC于点H，GH：GK的值是否改变？证明你发现的结论；
（3）三角板EFG由图①所示的位置绕O点逆时针旋转一周，是否存在某位置使△BFG是等腰三角形，若存在，请直接写出相应的旋转角α(精确到0.1°)；若不存在，说明理由．
【答案】(1) GH：GK=
；(2)不变，GH：GK=GN：GM=；(3)存在，30°、90°、133.2°或346.8°.
【解析】
（1）根据30°的直角三角形的三边关系，利用已知条件和勾股定理可以求出直角三角形的三边长度，利用三角形的中位线可以求出GK，和GH的值，可以求出其比值．
（2）作GM⊥AC于M，GN⊥BC于N，利用三角形相似可以求出GH与GK的比值不变．
（3）三角板EFG由图①所示的位置绕O点逆时针旋转一周，存在某位置使△BFG是等腰三角形，相应的旋转角α为：30°、90°、133.2°或346.8°.
（1）∵∠ACB=∠EGF=90°，∠B=∠F=30°
∴AC=
AB，EG=EF
∵AB=EF=4
∴AC=EG=2，在Rt△ACB和Rt△EGF中，由勾股定理得
BC=GF=2
∵GE⊥AC，GF⊥BC
∴GE∥BC，GF∥AC
∵G是AB的中点
∴K，H分别是AC、CB的中点
∴GK，GH是△ABC的中位线
∴GK=BC=，GH=AC=1
∴GH：GK=1；；
（2）不变，
理由如下：作GM⊥AC于M，GN⊥BC于N，
∴∠GMC=∠GNH=90°由旋转的性质可知：
∠2=∠1
∴△GMK∽△GNH
∴
∵GN：GM=1：
∴GH：GK=1：
∴旋转角α满足条件：0°＜α＜30°时，GH：GK的值比值不变；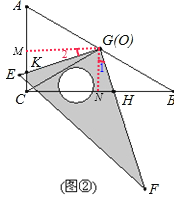
（3）三角板EFG由图①所示的位置绕O点逆时针旋转一周，存在某位置使△BFG是等腰三角形，相应的旋转角α为：30°、90°、133.2°或346.8°．
