题目内容
【题目】如图,在△ABC中,CD是高,CE是中线,CE=CB,点A、D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为 . 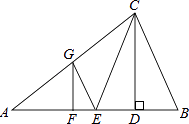
【答案】27
【解析】解:∵点A、D关于点F对称, ∴点F是AD的中点.
∵CD⊥AB,FG∥CD,
∴FG是△ACD的中位线,AC=18,BC=12,
∴CG= ![]() AC=9.
AC=9.
∵点E是AB的中点,
∴GE是△ABC的中位线,
∵CE=CB=12,
∴GE= ![]() BC=6,
BC=6,
∴△CEG的周长=CG+GE+CE=9+6+12=27.
故答案为:27.
先根据点A、D关于点F对称可知点F是AD的中点,再由CD⊥AB,FG∥CD可知FG是△ACD的中位线,故可得出CG的长,再根据点E是AB的中点可知GE是△ABC的中位线,故可得出GE的长,由此可得出结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目