题目内容
若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=-![]() ,x1•x2=
,x1•x2=![]() .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:AB=|x1-x2|=
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:AB=|x1-x2|=![]() =
=![]() =
=![]() =
=![]() ;
;
参考以上定理和结论,解答下列问题:
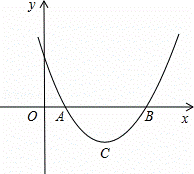
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.
考点:
抛物线与x轴的交点;根与系数的关系;等腰三角形的性质;等边三角形的性质。
分析:
(1)当△ABC为直角三角形时,由于AC=BC,所以△ABC为等腰直角三角形,过![]() C作CE⊥AB于E,则AB=2CE.根据本题定理和结论,得到AB=
C作CE⊥AB于E,则AB=2CE.根据本题定理和结论,得到AB=![]() ,根据顶点坐标公式,得到CE=|
,根据顶点坐标公式,得到CE=|![]() |=
|=![]() ,列出方程,解方程即可求出b2-4ac的值;
,列出方程,解方程即可求出b2-4ac的值;
(2)当△ABC为等边三角形时,解直角△ACE,得CE=![]() AE=
AE=![]() ,据此列出方程,解方程即可求出b2-4ac的值.
,据此列出方程,解方程即可求出b2-4ac的值.
解答:
解:(1)当△ABC为直角三角形时,过C作CE⊥AB于E,则AB=2CE.
∵抛物线与x轴有两个交点,△=b2-4ac>0,则|b2-4ac|=b2-4ac.
∵a>0,∴AB=![]() ,
,
又∵CE=|![]() |=
|=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵b2-4ac>0,
∴b2-4ac=4;
(2)当△ABC为等边三角形时,
由(1)可知CE=![]() ,
,
∴![]() ,
,
∵b2-4ac>0,
∴b2-4ac=12.

点评:
本题考查了等腰直角三角形、等边三角形的性质,抛物线与x轴的交点及根与系数的关系定理,综合性较强,难度中等.

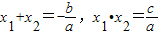 .我们把它们称为根与系数关系定理.
.我们把它们称为根与系数关系定理.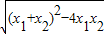 =
=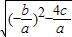 =
=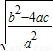 =
=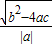
 .
.