题目内容
若反比例函数 的图象上有两点P1(1,y1)和P2(2,y2),那么( )
的图象上有两点P1(1,y1)和P2(2,y2),那么( )
| A.y2<y1<0 | B.y1<y2<0 | C.y2>y1>0 | D.y1>y2>0 |
D.
解析试题分析:把两点P1(1,y1)和P2(2,y2)分别代入反比例函数y= ,求出y2、y1的值即可作出判断.
,求出y2、y1的值即可作出判断.
解答:解:把点P1(1,y1)代入反比例函数y= 得,y1=1;
得,y1=1;
点P2(2,y2)代入反比例函数y= 求得,y2=
求得,y2= ,
,
∵1> >0,
>0,
∴y1>y2>0.
故选D.
考点: 反比例函数图象上点的坐标特征.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知反比例函数 的图象如图,则一元二次方程
的图象如图,则一元二次方程 根的情况是( )
根的情况是( )
| A.有两个不等实根 | B.有两个相等实根 | C.没有实根 | D.无法确定. |
反比例函数 的图象在( )
的图象在( )
| A.第一、三象限 | B.第二、四象限 |
| C.第一、二象限 | D.第三、四象限 |
下列各点在反比例函数 的图象上的是( )
的图象上的是( )
| A.(-1,-2) | B.(-1,2) | C.(-2,-1) | D.(2,1) |
已知点A(1,y1)、B(2,y2)、C(﹣3,y3)都在反比例函数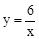 的图象上,则y1、y2、y3的大小关系是
的图象上,则y1、y2、y3的大小关系是
| A.y3<y1<y2 | B.y1<y2<y3 | C.y2<y1<y3 | D.y3<y2<y1 |
已知梯形的面积一定,它的高为h,中位线的长为x,则h与x的函数关系大致是
A. | B. | C. | D. |
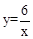 上,且OA=4,过A作AC⊥x轴,垂足为C, OA的垂直平分线交OC于B,则△ABC的周长为( )
上,且OA=4,过A作AC⊥x轴,垂足为C, OA的垂直平分线交OC于B,则△ABC的周长为( )



 )、B(-1,
)、B(-1, )、C(1,
)、C(1, )在反比例函数
)在反比例函数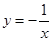 的图像上,则( )
的图像上,则( )






