题目内容
已知x1和x2是一元二次方程x2-5x-k=0的两个实数根,并且x1和x2满足不等式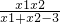 <4,则实数k的取值范围是________.
<4,则实数k的取值范围是________.
k≥-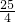
分析:根据根与系数的关系,先求得x1•x2、x1+x2的值,然后将其代入不等式,从而解得实数k的取值范围.
解答:∵x1和x2是一元二次方程x2-5x-k=0的两个实数根,
△=25+4k≥0,解得k≥-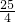 ,①
,①
∴x1•x2=-k,②
x1+x2=5,③
将②③代入不等式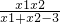 <4,得
<4,得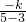 <4,即
<4,即 <4,
<4,
解得,k>-8,④
由①④,得
k≥-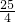 ;
;
故答案为:k≥-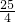 .
.
点评:本题主要考查了根与系数的关系、根的判别式及一元一次不等式的解法.在解不等式时一定要注意数值的正负与不等号的变化关系.
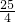
分析:根据根与系数的关系,先求得x1•x2、x1+x2的值,然后将其代入不等式,从而解得实数k的取值范围.
解答:∵x1和x2是一元二次方程x2-5x-k=0的两个实数根,
△=25+4k≥0,解得k≥-
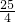 ,①
,①∴x1•x2=-k,②
x1+x2=5,③
将②③代入不等式
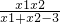 <4,得
<4,得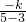 <4,即
<4,即 <4,
<4,解得,k>-8,④
由①④,得
k≥-
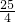 ;
;故答案为:k≥-
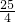 .
.点评:本题主要考查了根与系数的关系、根的判别式及一元一次不等式的解法.在解不等式时一定要注意数值的正负与不等号的变化关系.

练习册系列答案
相关题目
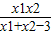 <4,则实数k的取值范围是 .
<4,则实数k的取值范围是 .