��Ŀ����
����Ŀ����ͼ����֪��BAD�͡�BCE��Ϊ����ֱ�������Σ���BAD=��BCE=90�㣬��MΪDE���е㣬����E��ADƽ�е�ֱ�߽�����AM�ڵ�N�� 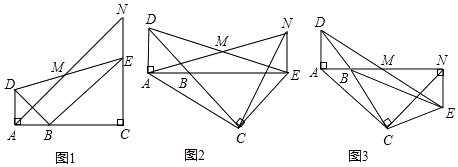
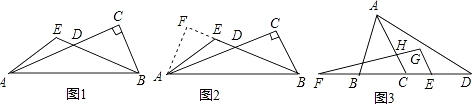
��1����A��B��C������ͬһֱ����ʱ����ͼ1������֤��MΪAN���е㣻
��2����ͼ1�С�BCE�Ƶ�B��ת����A��B��E������ͬһֱ���ϣ���ͼ2������֤����CANΪ����ֱ�������Σ�
��3����ͼ1�С�BCE�Ƶ�B��ת��ͼ3��λ��ʱ����2���еĽ����Ƿ���Ȼ����������������֤��֮��������������˵�����ɣ�
���𰸡�
��1���⣺֤������ͼ1����EN��AD��
���MAD=��MNE����ADM=��NEM��
�ߵ�MΪDE���е㣬
��DM=EM��
�ڡ�ADM�͡�NEM�У�
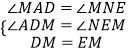 ��
��
���ADM�ա�NEM��AAS����
��AM=MN��
��MΪAN���е�
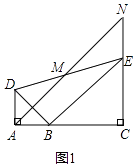
��2���⣺֤������ͼ2���ߡ�BAD�͡�BCE��Ϊ����ֱ�������Σ�
��AB=AD��CB=CE����CBE=��CEB=45�㣬
��AD��NE��
���DAE+��NEA=180�㣬
�ߡ�DAE=90�㣬
���NEA=90�㣬
���NEC=135�㣬
��A��B��E������ͬһֱ���ϣ�
���ABC=180�㩁��CBE=135�㣬
���ABC=��NEC��
�ߡ�ADM�ա�NEM����֤����
��AD=NE��
��AD=AB��
��AB=NE��
�ڡ�ABC�͡�NEC�У�
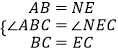 ��
��
���ABC�ա�NEC��SAS����
��AC=NC����ACB=��NCE��
�ߡ�BCE=90�㣬
���ACN=��BCE=90�㣬
���ACNΪ����ֱ�������Σ�
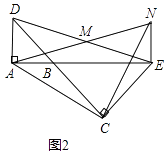
��3���⣺��ACN��Ϊ����ֱ�������Σ�
֤������ͼ3��A��B��N������ͬһ��ֱ���ϣ�
��AD��EN����DAB=90�㣬
���ENA=��DAN=90�㣬
�ߡ�BCE=90�㣬
���CBN+��CEN=360�㩁90�㩁90��=180�㣬
��A��B��N������ͬһ��ֱ���ϣ�
���ABC+��CBN=180�㣬
���ABC=��NEC��
�ߡ�ADM�ա�NEM����֤����
��AD=NE��
��AD=AB��
��AB=NE��
�ڡ�ABC�͡�NEC�У�
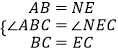 ��
��
���ABC�ա�NEC��SAS����
��AC=NC����ACB=��NCE��
���ACN=��BCE=90�㣬
���ACNΪ����ֱ�������Σ�
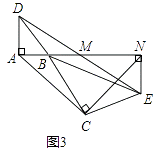
����������1����EN��AD�͵�MΪDE���е㣬����֤�á�ADM�ա�NEM���Ӷ�֤��MΪAN���е㣻��2��������֪��������֤AB=DA=NE����ABC=��NEC=135�㣬�Ӷ��ɵá�ABC�ա�NEC����������֤��AC=NC����ACN=��BCE=90�㣬�ɵá�ACNΪ����ֱ�������Σ���3��������֪�������á�ADM�ա�NEM�������ı���BCEF�ڽǺ�Ϊ360�㣬�ɵá�ABC=��FEC���Ӷ�����֤�á�ABC�ա�NEC����������֤��AC=NC����ACN=��BCE=90�㣬���ɵó���ACNΪ����ֱ�������Σ�
�����㾫�����������⣬������Ҫ�˽����ֱ��������(����ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45��)��

 �������Ͽ��㱾ϵ�д�
�������Ͽ��㱾ϵ�д�