题目内容
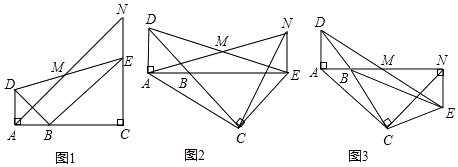
【题目】阅读下列材料： 如图1，在Rt△ABC中，∠C=90°，D为边AC上一点，DA=DB，E为BD延长线上一点，∠AEB=120°，猜想AC、BE、AE的数量关系，并证明．
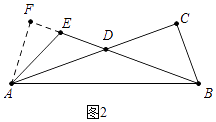
小明的思路是：根据等腰△ADB的轴对称性，将整个图形沿着AB边的垂直平分线翻折，得到点C的对称点F，如图2，过点A作AF⊥BE，交BE的延长线于F，请补充完成此问题；
参考小明思考问题的方法，解答下列问题：
如图3，等腰△ABC中，AB=AC，D、F在直线BC上，DE=BF，连接AD，过点E作EG∥AC交FH的延长线于点G，∠DFG+∠D=∠BAC．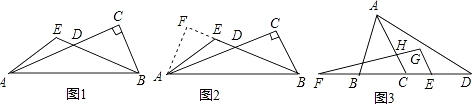
（1）探究∠BAD与∠CHG的数量关系；
（2）请在图中找出一条和线段AD相等的线段，并证明．
【答案】
（1）解：阅读材料，如图2中，结论：AC=BE+ 
AE．理由如下，
∵DA=DB，
∴∠DAB=∠DBA，
∵AF⊥BF，
∴∠F=∠C=90°，
在△ABF和△BAC中，
，
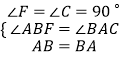∴△ABF≌△BAC，
∴AC=BF，
∵∠AEB=120°=∠F+∠FAE，
∴∠FAE=30°，∴EF= AE，
∴AC=BF=BE+EF=BE+ AE，
∴AC=BE+ AE．
问题：（1）如图3中，
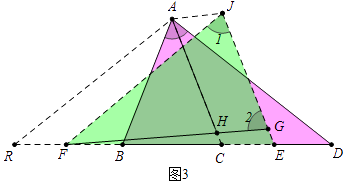
∵∠ACD=∠D+∠CAD，∠D+∠CFG=∠BAC，
∴∠CHG=∠CFH+∠FCH=∠CFH+∠D+∠CAD=∠BAC+∠CAD=∠BAD，
∴∠CHG=∠BAD．
（2）解：结论：AD=FG．理由如下，
如图3中，延长BF到R，使得BR=CD，连接AR，作AJ∥CD交EG的延长线于J，连接FJ．
∵AJ∥CE，AC∥JE，
∴四边形ACEJ，四边形ACGK是平行四边形，
∴AJ=CE，AC=JE，
∵AB=CA，
∴JE=AB，
∵AB=AC，
∴∠ABC=∠ACB，
∴∠ABR=∠ACD，
在△ABR和△ACD中，
，
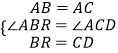∴△ABR≌△ACD，
∴AR=AD，
∵BR=CD，BF=ED，
∴FR=CE=AJ，EF=BD，∵AJ∥RF，
∴四边形ARFJ是平行四边形，
∴JF=AR=AD，
在△ABD和△JEF中，
，
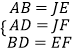∴△ABD≌△JEF，
∴∠1=∠BAD，
∵∠BAD=∠CHG=∠2，
∴∠1=∠2，
∴FG=FJ，
∴AD=FG．
【解析】阅读材料：如图2中，结论：AC=BE+ AE．理由如下，只要证明△ABF≌△BAC，推出AC=BF，再证明EF= AE，可得AC=BF=BE+EF=BE+ AE． 问题：（1）由∠ACD=∠D+∠CAD，∠D+∠CFG=∠BAC，推出∠CHG=∠CFH+∠FCH=∠CFH+∠D+∠CAD=∠BAC+∠CAD=∠BAD，可得∠CHG=∠BAD．（2）结论：AD=FG．如图3中，延长BF到R，使得BR=CD，连接AR，作AJ∥CD交EG的延长线于J，连接FJ．首先证明四边形ACEJ，四边形AJFR是平行四边形，再证明△ABD≌△JEF，想办法证明∠1=∠2，即可解决问题．
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°，以及对线段垂直平分线的性质的理解，了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等．
