Question

【题目】如图，在△ABC中，AB=AC=10cm，BC=12cm，点P从点C出发，在线段CB上以每秒1cm的速度向点B匀速运动．与此同时，点M从点B出发，在线段BA上以每秒lcm的速度向点A匀速运动．过点P作PN⊥BC，交AC点N，连接MP，MN．当点P到达BC中点时，点P与M同时停止运动．设运动时间为t秒（t＞0）．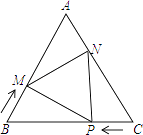

（1）当t为何值时，PM⊥AB．
（2）设△PMN的面积为y（cm2），求出y与x之间的函致关系式．
（3）是否存在某一时刻t，使S△PMN：S△ABC=1：5？若存在，求出t的值；若不存在，说明理由．

Answer 1

【答案】
（1）

解：过点A作AD⊥BC于D，

∵AB=AC，∠ADB=90°，

∴BD=CD=6，

∴ =8，

∵MP⊥AB，

∴∠BMP=∠ADB=90°，

∵∠B=∠B，

∴△BMP∽△BDA，

∴ ，

∴ 解得t= ，

∴当t为 时，PM⊥AB

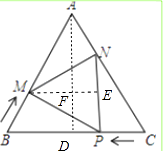
（2）

解：过点M作ME⊥NP于E，交AD于F．

∵BC⊥NP，

∴NP∥AD，

∴∠ADP=∠C，

∵∠C=∠NPC，

∴△BMP∽△BDA，

∴ ，

∴ ，

∴PN= ，同理MF= ，

∵∠BPN=∠ADP=∠MEP=90°，

∴四边形DPEF是矩形，

∴EF=DP=6﹣t，

∴ME=MF+EF= （10﹣t）+6﹣t=12﹣ ，

∴S△MPN= PNME= =﹣ +8t，（0＜t≤6）

（3）

解：存在．

由题意：﹣ +8t= × ×12×8，

解得到t= 或6．

所以t= 秒或6秒时，S△PMN：S△ABC=1：5．

【解析】（1）根据△BMP∽△BDA得 即可列出方程解决．（2）根据△BMP∽△BDA得 求出PN，MF，在证明四边形DPEF是矩形得到ME即可．（3）代入（2）即可用方程解决．
【考点精析】根据题目的已知条件，利用相似图形和相似三角形的性质的相关知识可以得到问题的答案，需要掌握形状相同，大小不一定相同（放大或缩小）;判定:①平行；②两角相等；③两边对应成比例，夹角相等；④三边对应成比例；对应角相等，对应边成比例的两个三角形叫做相似三角形．