题目内容
如图,直线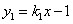 与x轴正半轴交于点A(2,0),以OA为边在x轴上方作正方形OABC,延长CB交直线
与x轴正半轴交于点A(2,0),以OA为边在x轴上方作正方形OABC,延长CB交直线 于点D,再以BD为边向上作正方形BDEF.
于点D,再以BD为边向上作正方形BDEF.

(1)求点F的坐标;
(2)设直线OF的解析式为 ,若
,若 ,求x的取值范围.
,求x的取值范围.
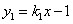 与x轴正半轴交于点A(2,0),以OA为边在x轴上方作正方形OABC,延长CB交直线
与x轴正半轴交于点A(2,0),以OA为边在x轴上方作正方形OABC,延长CB交直线 于点D,再以BD为边向上作正方形BDEF.
于点D,再以BD为边向上作正方形BDEF.
(1)求点F的坐标;
(2)设直线OF的解析式为
 ,若
,若 ,求x的取值范围.
,求x的取值范围.(1)(2,6);(2)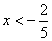
试题分析:(1)将A(2,0)代入
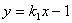 得
得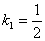 ,根据正方形的性质可得BC=OC=AB=OA=2,则在
,根据正方形的性质可得BC=OC=AB=OA=2,则在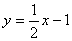 中,当
中,当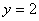 时,
时,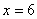 ,即得CD、BD的长,再根据正方形的性质可得BF的长;
,即得CD、BD的长,再根据正方形的性质可得BF的长;(2)将(1)中求得的点F的坐标代入
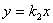 ,得
,得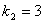 ,由
,由 可得关于x的不等式.
可得关于x的不等式.(1)将A(2,0)代入
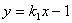 得:
得: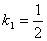
∵四边形OABC是正方形
∴BC=OC=AB=OA=2
在
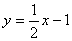 中,当
中,当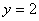 时,
时,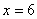
∴CD=6
∴BD=CD-BC=6-2=4
∵四边形BDEF是正方形
∴BF=BD=4
∴AF=AB+BF=2+4=6
∴点F的坐标为(2,6);
(2)将F(2,6)代入
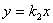 ,得
,得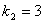
∵

∴
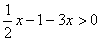
解得
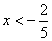 .
.点评:待定系数法求函数关系式是初中数学的重点,在中考中极为常见,一般难度不大,需熟练掌握.

练习册系列答案
相关题目

 上的一点,过点M作x轴、y轴的垂线,分别交直线y=-2x+m于D、C两点,若直线y=-2x+m与y轴交于点A,与x轴相交于点B.则AD·BC的值为
上的一点,过点M作x轴、y轴的垂线,分别交直线y=-2x+m于D、C两点,若直线y=-2x+m与y轴交于点A,与x轴相交于点B.则AD·BC的值为 
 (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),A点的横坐标为-1.
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),A点的横坐标为-1.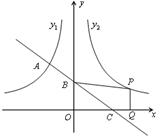
 (x>0)的图象与
(x>0)的图象与 (x<0)的图象关于y轴对称,在
(x<0)的图象关于y轴对称,在 ?
? ,点E是AD的三等分点,且AE
,点E是AD的三等分点,且AE DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为
DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为 .
.
 为等腰三角形?若存在,请直接写出时间
为等腰三角形?若存在,请直接写出时间 与四边形
与四边形 的重叠部分的面积为S,试求S与
的重叠部分的面积为S,试求S与 分别表示乌龟和兔子所行的路程,t为时间,则下列图像中与故事相吻合的是( )
分别表示乌龟和兔子所行的路程,t为时间,则下列图像中与故事相吻合的是( )