题目内容
已知抛物线的函数解析式为y=ax2+b x-3a(b<0),若这条抛物线经过点(0,-3),方程ax2+b x-3a=0的两根为x1,x2,且|x1-x2|=4.
⑴求抛物线的顶点坐标.
⑵已知实数x>0,请证明x+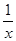 ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+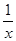 =2.
=2.
⑴求抛物线的顶点坐标.
⑵已知实数x>0,请证明x+
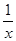 ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+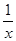 =2.
=2.(1)抛物线的顶点坐标为(1,-4) (2)

试题分析:解:(1)∵抛物线过(0,-3)点,∴-3a=-3 ∴a=1 ∴y=x2+b x-3
∵x2+b x-3=0的两根为x1,x2, ∴
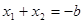 ,
,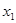 ·
·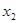 =-3
=-3∵
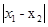 =4∴
=4∴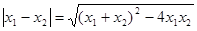 =4
=4 ∴
 ∴
∴ ∵b<0 ∴b=-2
∵b<0 ∴b=-2 ∴y=x2-2x-3=(x-1)2-4 ∴抛物线的顶点坐标为(1,-4)
(2)∵x>0,∴

∴
 显然当x=1时,才有
显然当x=1时,才有
点评:该题是常考题,主要考查学生对二次函数系数的求取以及顶点的求解方法,要求学生掌握三次函数的一般表达式、顶点式和交点式。

练习册系列答案
相关题目
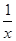 -2实数根的情况是
-2实数根的情况是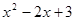 )图象上的最低点是__ .
)图象上的最低点是__ . 与x轴的交点坐标是(-l,0)和(3,0),则此抛物线的对称轴是
与x轴的交点坐标是(-l,0)和(3,0),则此抛物线的对称轴是 x2+x+
x2+x+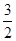
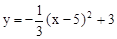 ,下列说法正确的是
,下列说法正确的是 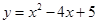 化成
化成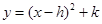 的形式,则
的形式,则 = .
= .