题目内容
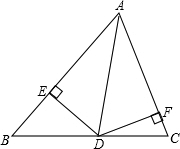
10、如图所示在三角形△ABC中AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F，则下列四个结论中，①AB上一点与AC上一点到D的距离相等；②AD上任意一点到AB、AC的距离相等；③∠BDE=∠CDF；④BD=CD，AD⊥BC．其中正确的个数是（ ）分析：利用角平分线上的点到角两边的距离相等，得①、②正确；通过证明△BED≌△CFD，可得到③中的结论；利用等腰三角形底边上的中线、高线与顶角的角平分线三线合一，可得④中的结论．
解答：解：①∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F，∴DE=DF，∴①AB上一点与AC上一点到D的距离相等；
②∵AD是△ABC的角平分线，角平分线上的点到角两边的距离相等，∴AD上任意一点到AB、AC的距离相等；
③∵AB=AC，∴∠B=∠C，又∵∠BED=∠CFD，DE=DF，∴△BED≌△CFD，∴BDE=∠CDF；
④∵AB=AC，AD是△ABC的角平分线，∴BD=CD，AD⊥BC．
所以①、②、③、④均正确，故选D．
②∵AD是△ABC的角平分线，角平分线上的点到角两边的距离相等，∴AD上任意一点到AB、AC的距离相等；
③∵AB=AC，∴∠B=∠C，又∵∠BED=∠CFD，DE=DF，∴△BED≌△CFD，∴BDE=∠CDF；
④∵AB=AC，AD是△ABC的角平分线，∴BD=CD，AD⊥BC．
所以①、②、③、④均正确，故选D．
点评：本题考查了等腰三角形的性质、全等三角形的判定及其性质等知识．根据相关知识对各选项进行逐个验证是正确解答本题的关键．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
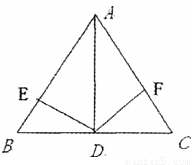
如图所示在三角形△ABC中AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F，则下列四个结论中，①AB上有一点与AC上一点到D的距离相等；②AD上任意一点到AB、AC的距离相等；③∠BDE=∠CDF；④BD=CD，AD⊥BC．其中正确的个数是
