题目内容
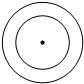如图，在以O为圆心的两个圆中，大圆的半径为5，小圆的半径为3，则与小圆相切的大圆的弦长为
- A.4
- B.6
- C.8
- D.10
C
分析：利用小圆半径，大圆半径和弦的一半构造直角三角形，利用勾股定理可求算出弦的一半的长，再求弦长．
解答：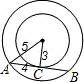
解：∵AB是小圆的切线，
∴OC⊥AB，
∴AB=2AC，
如图，在直角△AOC中，根据勾股定理可得：OC=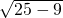
=
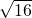=4，所以弦长为8．故选C．
点评：利用垂径定理可用同心圆的两个半径和与小圆相切的大圆的弦的一半构造直角三角形，运用勾股定理解题是常用的一种方法，要掌握．
分析：利用小圆半径，大圆半径和弦的一半构造直角三角形，利用勾股定理可求算出弦的一半的长，再求弦长．
解答：
解：∵AB是小圆的切线，∴OC⊥AB，
∴AB=2AC，
如图，在直角△AOC中，根据勾股定理可得：OC=
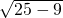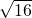==4，所以弦长为8．故选C．点评：利用垂径定理可用同心圆的两个半径和与小圆相切的大圆的弦的一半构造直角三角形，运用勾股定理解题是常用的一种方法，要掌握．
练习册系列答案
相关题目
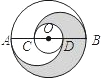如图，在以O为圆心的两个同心圆中，大圆的直径AB交小圆于C、D两点，AC=CD=DB，分别以C、D为圆心，以CD为半径作圆．若AB=6cm，则图中阴影部分的面积为
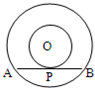9、如图，在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点，已知AB=8，大圆半径为5，则小圆半径为（ ）
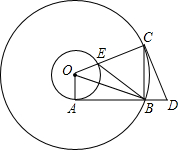（2006•静安区二模）如图，在以O为圆心的两个同心圆中，小圆的半径为1，AB与小圆相切于点A，与大圆相交于B，大圆的弦BC⊥AB，过点C作大圆的切线交AB的延长线于D，OC交小圆于E
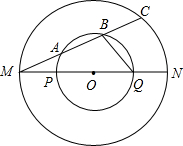如图，在以O为圆心的两个同心圆中，MN为大圆的直径，交小圆于点P、Q，大圆的弦MC交小圆于点A、B．若OM=2，OP=1，MA=AB=BC，则△MBQ的面积为
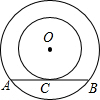如图，在以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆的半径为5cm，小圆的半径为3cm，则弦AB的长为（ ）