题目内容
(2005•泰安)某“研究性学习小组”遇到了以下问题,请参与:已知,△ABC是等边三角形且内接于⊙O,取
 上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.
上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.
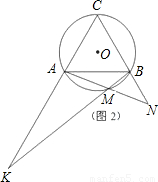

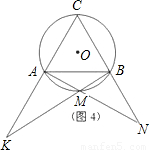
(1)如图1,图2,图3,M分别为
 的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:
的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:| △ABC的边长 | AK•BN的值 | |
| 图1 | 2 | |
| 图2 | 2 | |
| 图3 | 2 |
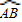 上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为______;
上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为______;(3)对(2)中提出的猜想,依图4给出证明.
【答案】分析:本题要求的实际是AK、BN与等边三角形ABC边长的关系.可通过证△AKB与△BAN相似来求解.
解答: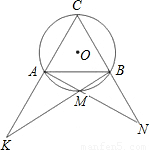 解:(1)4,4,4
解:(1)4,4,4
(2)AK•BN=AB2
(3)∵∠ABM+∠BAM=∠AMK=∠C=60°,∠BAM+∠N=60°
∴∠ABM=∠N
∵∠KAB=∠NBA=120°
∴△AKB∽△BAN
∴
∴AK•BN=AB2.
点评:本题主要考查了圆周角定理,相似三角形的判定和性质,等边三角形的性质等知识点.根据圆周角定理得出角相等从而证得三角形相似是解题的关键.
解答:
 解:(1)4,4,4
解:(1)4,4,4(2)AK•BN=AB2
(3)∵∠ABM+∠BAM=∠AMK=∠C=60°,∠BAM+∠N=60°
∴∠ABM=∠N
∵∠KAB=∠NBA=120°
∴△AKB∽△BAN
∴

∴AK•BN=AB2.
点评:本题主要考查了圆周角定理,相似三角形的判定和性质,等边三角形的性质等知识点.根据圆周角定理得出角相等从而证得三角形相似是解题的关键.

练习册系列答案
相关题目
(2005•泰安)某“研究性学习小组”遇到了以下问题,请参与:
已知,△ABC是等边三角形且内接于⊙O,取 上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.
上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.

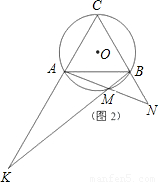
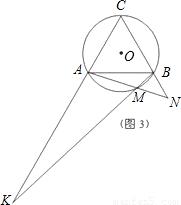
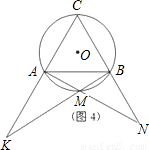
(1)如图1,图2,图3,M分别为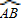 的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:
的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:
(2)如图4,当M为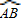 上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为______;
上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为______;
(3)对(2)中提出的猜想,依图4给出证明.
已知,△ABC是等边三角形且内接于⊙O,取
 上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.
上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.



(1)如图1,图2,图3,M分别为
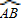 的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:
的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:| △ABC的边长 | AK•BN的值 | |
| 图1 | 2 | |
| 图2 | 2 | |
| 图3 | 2 |
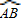 上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为______;
上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为______;(3)对(2)中提出的猜想,依图4给出证明.
(2005•泰安)某“希望学校”为加强信息技术课教学,拟投资建一个初级计算机房和一个高级计算机房,每个机房只配置1台教师用机,若干台学生用机.现有厂方提供的产品推介单一份,如下表.
现知:教师配置CZXM系列机型,学生配置CZXN系列机型;所有机型均按八折优惠销售,两个机房购买计算机的钱数相等,并且每个机房购买计算机的钱数不少于20万元也不超过21万元.
请计算,拟建的两个机房各能配置多少台学生用机?
现知:教师配置CZXM系列机型,学生配置CZXN系列机型;所有机型均按八折优惠销售,两个机房购买计算机的钱数相等,并且每个机房购买计算机的钱数不少于20万元也不超过21万元.
请计算,拟建的两个机房各能配置多少台学生用机?
| 类别 | 初级机房 | 高级机房 |
| 机型 | CZXM-012型 | CZXM-025型 |
| CZXN-316型 | CZXN-216型 | |
| 生产日期 | 2005年1月 | 2005年3月 |
| 单价 | CZXM-012型 10000元 | CZXM-025型 14375元 |
| CZXN-316型 4375元 | CZXN-216型 8750元 | |
| 性能 | 多人交互… | … |
| … | … | … |

