题目内容
 如图,已知在△ABC中,AD=2,DB=4,DE∥BC.设
如图,已知在△ABC中,AD=2,DB=4,DE∥BC.设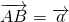 ,
,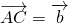 ,试用向量
,试用向量 、
、 表示向量
表示向量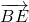 =________.
=________.

分析:首先由DE∥BC,得到△ADE∽△ABC,由
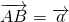 ,
,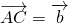 ,即可求得
,即可求得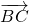 ,由相似三角形的对应边成比例,即可得到
,由相似三角形的对应边成比例,即可得到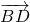 ,
,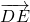 ;即可求得
;即可求得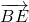 .
.解答:∵AD=2,DB=4,DE∥BC,
∴△ADE∽△ABC,AB=AD+DB=6,
∴
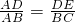 =
= ,
,∴BD=
 BA,DE=
BA,DE= BC,
BC,∵
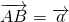 ,
,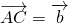 ,
,∴
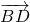 =-
=-
 ,
,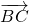 =
=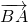 +
+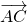 =-
=- +
+ ,
,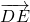 =
=
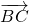 =
= (-
(- +
+ ),
),∴
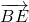 =
=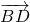 +
+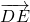 =-
=-
 +
+ (-
(- +
+ )=-
)=-
 -
-
 +
+
 =
=
 -
- .
.故答案为:

 -
- .
.点评:此题考查了相似三角形的判定与性质,以及向量的意义与计算.此题难度比较大,解题时要注意数形结合思想的应用.

练习册系列答案
相关题目
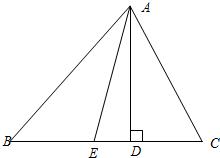
 如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.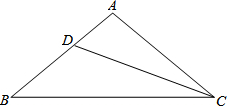 如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线.
如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线.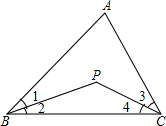 如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为
如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为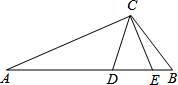 如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.
如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.