题目内容
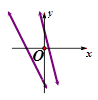
(本题10分) 如图,直线 与反比例函数
与反比例函数 的图象交于A
的图象交于A ,B
,B 两点.
两点.

(1)求 、
、 的值?
的值?
(2)直接写出 时x的取值范围?
时x的取值范围?
(3)如图,等腰梯形OBCD中,BC//OD,OB=CD,OD边在x轴上,过点C作CE
⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,
请判断PC和PE的大小关系,并说明理由.
 与反比例函数
与反比例函数 的图象交于A
的图象交于A ,B
,B 两点.
两点.
(1)求
 、
、 的值?
的值?(2)直接写出
 时x的取值范围?
时x的取值范围?(3)如图,等腰梯形OBCD中,BC//OD,OB=CD,OD边在x轴上,过点C作CE
⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,
请判断PC和PE的大小关系,并说明理由.
(1) 解:由题意:k2=1×6=6………………1分
∴反比例函数的解析式为: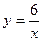
又∵B(a,3)在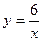 的图象上,
的图象上,
∴a="2 " B(2,3)………………………………1分
∵直线 过点A
过点A ,B(2,3)
,B(2,3)
∴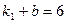
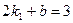 解得:k1=-3 b=9………………2分
解得:k1=-3 b=9………………2分
(2) x的取值范围:1<x<2………………………2分
(3) 判断PC=PE………………………………………………………………1分
设点P的坐标为(m,n)
∵BC∥OD, CE⊥OD BO=CD, B(2,3),
∴C(m,3), CE=3, BC=m-2, OD=m+2
∴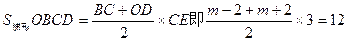
∴m=4………………………………………………………………………2分
又∵mn=6 ∴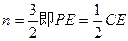 ……………………………1分
……………………………1分
∴判断PC=PE
∴反比例函数的解析式为:
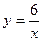
又∵B(a,3)在
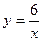 的图象上,
的图象上,∴a="2 " B(2,3)………………………………1分
∵直线
 过点A
过点A ,B(2,3)
,B(2,3)∴
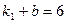
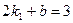 解得:k1=-3 b=9………………2分
解得:k1=-3 b=9………………2分(2) x的取值范围:1<x<2………………………2分
(3) 判断PC=PE………………………………………………………………1分
设点P的坐标为(m,n)
∵BC∥OD, CE⊥OD BO=CD, B(2,3),
∴C(m,3), CE=3, BC=m-2, OD=m+2
∴
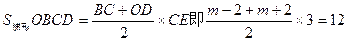
∴m=4………………………………………………………………………2分
又∵mn=6 ∴
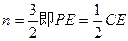 ……………………………1分
……………………………1分∴判断PC=PE
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
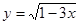 中自变量x的取值范围是
中自变量x的取值范围是 
 年后该地剩余绿地面积为
年后该地剩余绿地面积为 万公顷. 在下列图象中, 能正确反映
万公顷. 在下列图象中, 能正确反映

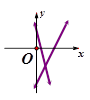
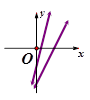
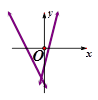
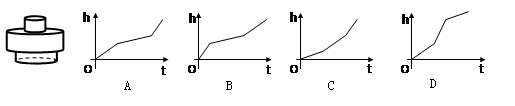
 在同一直角坐标系中的图象大致是( )
在同一直角坐标系中的图象大致是( ) 
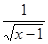 自变量x的取值范围是 。
自变量x的取值范围是 。