题目内容
如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE:EB=4:1,EF⊥AC于F,连接FB,则sin∠BFC的值等于______.
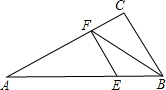

∵Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE:EB=4:1,
∴BC=
AB,
设AB=5x,
∵AE:EB=4:1,
∴AE=4x,EB=x,BC=
,
∵△ABC是直角三角形,
∴AC=
=
=
x,
∵EF⊥AC,
∴EF∥BC,AF:FC=AE:BE=4:1,即FC=
AC=
×
x=
x,
∴BF=
=
=
x,
∴sin∠BFC=
=
×
=
.
故答案为:
.
∴BC=
| 1 |
| 2 |
设AB=5x,
∵AE:EB=4:1,
∴AE=4x,EB=x,BC=
| 5x |
| 2 |
∵△ABC是直角三角形,
∴AC=
| AB2-BC2 |
(5x)2-(
|
5
| ||
| 2 |
∵EF⊥AC,
∴EF∥BC,AF:FC=AE:BE=4:1,即FC=
| 1 |
| 5 |
| 1 |
| 5 |
5
| ||
| 2 |
| ||
| 2 |
∴BF=
| BC2+FC2 |
(
|
| 7 |
∴sin∠BFC=
| BC |
| BF |
| 5x |
| 2 |
| 1 | ||
|
5
| ||
| 14 |
故答案为:
5
| ||
| 14 |

练习册系列答案
相关题目
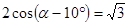 ,则锐角
,则锐角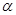 的度数是 °
的度数是 °