题目内容
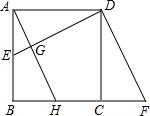 已知:如图,在正方形ABCD中,E是AB上的一点,延长BC到F使CF=AE,把△DCF向左平移,使DC与AB重合,得到△ABH,AH交DE于点G.
已知:如图,在正方形ABCD中,E是AB上的一点,延长BC到F使CF=AE,把△DCF向左平移,使DC与AB重合,得到△ABH,AH交DE于点G.
求证:AH⊥DE.
证明:∵四边形ABCD是平行四边形,
∴AD=DC,∠DAB=∠BCD=90°,
∴∠DCF=90°,
∴∠DAB=∠DCF,
∵AE=CF,
∴△ADE≌△DCF,
∵把△DCF向左平移得到△ABH,
∴△ABH≌△DCF,
∴△DAE≌△ABH,
∴∠ADE=∠BAH,
∵∠BAH+∠GAD=∠BAD=90°,
∴∠ADE+∠GAD=90°,
∴∠AGD=180°-(∠ADE+∠GAD)=90°,
∴AH⊥DE.
分析:根据平行四边形性质得出AD=DC,∠DAB=∠BCD=90°,根据SAS证△ADE≌△DCF,根据平移性质得出△ABH≌△DCF,推出△DAE≌△ABH,求出∠ADE=∠BAH,求出∠ADE+∠GAD=90°,
根据三角形的内角和定理求出∠AGD=90°,根据垂线定义得出即可.
点评:本题考查了正方形性质,全等三角形的性质和判定,垂线,平移的性质等知识点的运用,解此题的关键是根据这些性质求出∠ADE+∠GAD=90°,题目综合性比较强,培养了学生综合运用性质进行推理的能力.
∴AD=DC,∠DAB=∠BCD=90°,
∴∠DCF=90°,
∴∠DAB=∠DCF,
∵AE=CF,
∴△ADE≌△DCF,
∵把△DCF向左平移得到△ABH,
∴△ABH≌△DCF,
∴△DAE≌△ABH,
∴∠ADE=∠BAH,
∵∠BAH+∠GAD=∠BAD=90°,
∴∠ADE+∠GAD=90°,
∴∠AGD=180°-(∠ADE+∠GAD)=90°,
∴AH⊥DE.
分析:根据平行四边形性质得出AD=DC,∠DAB=∠BCD=90°,根据SAS证△ADE≌△DCF,根据平移性质得出△ABH≌△DCF,推出△DAE≌△ABH,求出∠ADE=∠BAH,求出∠ADE+∠GAD=90°,
根据三角形的内角和定理求出∠AGD=90°,根据垂线定义得出即可.
点评:本题考查了正方形性质,全等三角形的性质和判定,垂线,平移的性质等知识点的运用,解此题的关键是根据这些性质求出∠ADE+∠GAD=90°,题目综合性比较强,培养了学生综合运用性质进行推理的能力.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
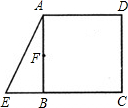 已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=
已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=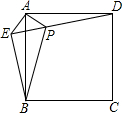 已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=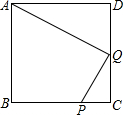 已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似? 、CE、CB于点F、H、G,交AB的延长线于点P.
、CE、CB于点F、H、G,交AB的延长线于点P. 已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.
已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.