题目内容
已知△ABC为等边三角形,AB=6,P是AB上的一个动点(与A、B不重合),过点P作AB的垂线与BC相交于点D,以点D为正方形的一个顶点,在△ABC内作正方形DEFG,其中D、E在BC上,F在AC上,
(1)设BP的长为x,正方形DEFG的边长为y,写出y关于x的函数解析式及定义域;
(2)当BP=2时,求CF的长;
(3)△GDP是否可能成为直角三角形?若能,求出BP的长;若不能,请说明理由.
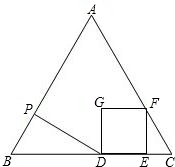
(1)设BP的长为x,正方形DEFG的边长为y,写出y关于x的函数解析式及定义域;
(2)当BP=2时,求CF的长;
(3)△GDP是否可能成为直角三角形?若能,求出BP的长;若不能,请说明理由.

(1)∵△ABC为等边三角形,
∴∠B=∠C=60°,AB=BC=AC=6.(1分)
∵DP⊥AB,BP=x,
∴BD=2x.(1分)
又∵四边形DEFG是正方形,
∴EF⊥BC,EF=DE=y,
∴EC=
y.(1分)
∴2x+y+
y=6,(2分)
∴y=(
-3)x+9-3
.(1分)
(6-3
≤x<3)(1分)
(2)当BP=2时,y=(
-3)×2+9-3
=3-
.(1分)
CF=
=2
-2.(1分)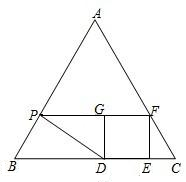
(3)△GDP能成为直角三角形.(1分)
①∠PGD=90°时,
6-x=
y+y,6-x=(
+1)•[(
-3)x+9-3
],
得到:x=
.(2分)
②∠GPD=90°时,G在AB上,参照(1).

∴∠B=∠C=60°,AB=BC=AC=6.(1分)
∵DP⊥AB,BP=x,
∴BD=2x.(1分)
又∵四边形DEFG是正方形,
∴EF⊥BC,EF=DE=y,
∴EC=
| ||
| 3 |
∴2x+y+
| ||
| 3 |
∴y=(
| 3 |
| 3 |
(6-3
| 3 |
(2)当BP=2时,y=(
| 3 |
| 3 |
| 3 |
CF=
| 2y | ||
|
| 3 |

(3)△GDP能成为直角三角形.(1分)
①∠PGD=90°时,
6-x=
| 3 |
| 3 |
| 3 |
| 3 |
得到:x=
30-6
| ||
| 11 |
②∠GPD=90°时,G在AB上,参照(1).


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目