题目内容
在Rt△ABC中,∠C=90°,AC=6,BC=8,若以C为圆心,R为半径所作的圆与斜边AB只有一个公共点,则R的取值范围是________.
R=4.8或6<R≤8
分析:画出符合条件的图形,①根据切线性质和三角形的面积即可求出答案;②画出图形,根据图形即可得出答案.
解答:由勾股定理得:AB=10,
分为两种情况:①如图1,当⊙C与AB相切时,只有一个公共点,

则CD⊥AB,
由三角形的面积公式得:S△ABC= ×AC×BC=
×AC×BC= ×AB×CD,
×AB×CD,
∴6×8=10×CD,
CD=4.8,
即R=4.8,
②如图2,当R的范围是6<R≤8时,⊙C和AB只有一个公共点,

故答案为:R=4.8或6<R≤8.
点评:本题考查了直线与圆的位置关系和三角形的面积等知识点,解此题的关键是画出符合条件的所有情况.
分析:画出符合条件的图形,①根据切线性质和三角形的面积即可求出答案;②画出图形,根据图形即可得出答案.
解答:由勾股定理得:AB=10,
分为两种情况:①如图1,当⊙C与AB相切时,只有一个公共点,

则CD⊥AB,
由三角形的面积公式得:S△ABC=
 ×AC×BC=
×AC×BC= ×AB×CD,
×AB×CD,∴6×8=10×CD,
CD=4.8,
即R=4.8,
②如图2,当R的范围是6<R≤8时,⊙C和AB只有一个公共点,

故答案为:R=4.8或6<R≤8.
点评:本题考查了直线与圆的位置关系和三角形的面积等知识点,解此题的关键是画出符合条件的所有情况.

练习册系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
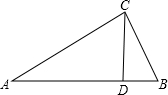 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
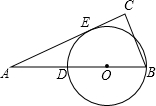 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.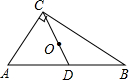 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )