题目内容
(2013•朝阳区一模)在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.
(1)如图1,求证:ME=MF;
(2)如图2,点G是线段BC上一点,连接GE、GF、GM,若△EGF是等腰直角三角形,∠EGF=90°,求AB的长;
(3)如图3,点G是线段BC延长线上一点,连接GE、GF、GM,若△EGF是等边三角形,则AB=

(1)如图1,求证:ME=MF;
(2)如图2,点G是线段BC上一点,连接GE、GF、GM,若△EGF是等腰直角三角形,∠EGF=90°,求AB的长;
(3)如图3,点G是线段BC延长线上一点,连接GE、GF、GM,若△EGF是等边三角形,则AB=
2
| 3 |
2
.| 3 |

分析:(1)根据ABCD是矩形,得出∠EAM=∠FDM=90°,根据AM=DM,∠AME=∠FMD证出△AEM≌△DFM,即可得出ME=FM;
(2)过点G作GH⊥AD于H,则AB=GH,根据△GEF是等腰直角三角形,得出ME=FM,GM⊥EF,根据∠MGE=∠MGF=45°,∠AME+∠GMH=90°,得出∠MGE=∠MEG=45°,ME=MG,再根据∠AME+∠AEM=90°,得出∠AEM=∠GMH从而证出△AEM≌△HMG,得出GH=AM=2,求出AB=2;
(3)过点G作GH⊥AD交AD延长线于点H,连接MG,则∠GHM=∠A,根据△GEF是等边三角形,得出EM=FM,GM⊥EF,
=cot60°=
,∠AME+∠GMH=90°,根据∠AME+∠AEM=90°,得出∠GMH=∠AEM,证出△AEM∽△HMG,
=
=
,得出HG=
AM=2
,最后根据AB=HG即可求出答案.
(2)过点G作GH⊥AD于H,则AB=GH,根据△GEF是等腰直角三角形,得出ME=FM,GM⊥EF,根据∠MGE=∠MGF=45°,∠AME+∠GMH=90°,得出∠MGE=∠MEG=45°,ME=MG,再根据∠AME+∠AEM=90°,得出∠AEM=∠GMH从而证出△AEM≌△HMG,得出GH=AM=2,求出AB=2;
(3)过点G作GH⊥AD交AD延长线于点H,连接MG,则∠GHM=∠A,根据△GEF是等边三角形,得出EM=FM,GM⊥EF,
| EM |
| GM |
| ||
| 3 |
| AM |
| HG |
| EM |
| GM |
| ||
| 3 |
| 3 |
| 3 |
解答: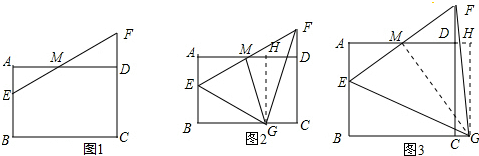 解:(1)如图1,
解:(1)如图1,
∵ABCD是矩形,
∴∠EAM=∠FDM=90°,
∵M是AD的中点,
∴AM=DM,
∵在△AEM和△DFM中,
,
∴△AEM≌△DFM(ASA),
∴ME=FM.
(2)如图2:
过点G作GH⊥AD于H,则AB=GH,
∵△GEF是等腰直角三角形,ME=FM,
∴GM⊥EF,
∴∠MGE=∠MGF=45°,∠AME+∠GMH=90°,
∴∠MGE=∠MEG=45°,
∴ME=MG,
∵∠AME+∠AEM=90°,
∴∠AEM=∠GMH,
∵在△AEM和△HMG中,
,
∴△AEM≌△HMG(AAS),
∴GH=AM=2,
∴AB=2.
(3)如图3:
过点G作GH⊥AD交AD延长线于点H,连接MG,则∠GHM=∠A,
∵△GEF是等边三角形,EM=FM,
∴GM⊥EF,
∴
=cot60°=
,
∠AME+∠GMH=90°,
∵∠AME+∠AEM=90°,
∴∠GMH=∠AEM,
∴△AEM∽△HMG,
∴
=
=
,
∴HG=
AM=2
,
∴AB=HG=2
.
故答案为:2
.
 解:(1)如图1,
解:(1)如图1,∵ABCD是矩形,
∴∠EAM=∠FDM=90°,
∵M是AD的中点,
∴AM=DM,
∵在△AEM和△DFM中,
|
∴△AEM≌△DFM(ASA),
∴ME=FM.
(2)如图2:
过点G作GH⊥AD于H,则AB=GH,
∵△GEF是等腰直角三角形,ME=FM,
∴GM⊥EF,
∴∠MGE=∠MGF=45°,∠AME+∠GMH=90°,
∴∠MGE=∠MEG=45°,
∴ME=MG,
∵∠AME+∠AEM=90°,
∴∠AEM=∠GMH,
∵在△AEM和△HMG中,
|
∴△AEM≌△HMG(AAS),
∴GH=AM=2,
∴AB=2.
(3)如图3:
过点G作GH⊥AD交AD延长线于点H,连接MG,则∠GHM=∠A,
∵△GEF是等边三角形,EM=FM,
∴GM⊥EF,
∴
| EM |
| GM |
| ||
| 3 |
∠AME+∠GMH=90°,
∵∠AME+∠AEM=90°,
∴∠GMH=∠AEM,
∴△AEM∽△HMG,
∴
| AM |
| HG |
| EM |
| GM |
| ||
| 3 |
∴HG=
| 3 |
| 3 |
∴AB=HG=2
| 3 |
故答案为:2
| 3 |
点评:此题考查了四边形综合,用到的知识点是全等三角形的判定及性质,相似三角形的判定及性质,三角函数值的运用,等边三角形、等腰直角三角形的性质.在解答时添加辅助线构建全等形和相似形是关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 (2013•朝阳区一模)如图,矩形ABCD的两条对角线相交于点O,∠BOC=120°,AB=3,一动点P以1cm/s的速度沿折线OB-BA运动,那么点P的运动时间x(s)与点C、O、P围成的三角形的面积y之间的函数图象为( )
(2013•朝阳区一模)如图,矩形ABCD的两条对角线相交于点O,∠BOC=120°,AB=3,一动点P以1cm/s的速度沿折线OB-BA运动,那么点P的运动时间x(s)与点C、O、P围成的三角形的面积y之间的函数图象为( ) (2013•朝阳区一模)已知:一次函数y=x+2与反比例函数y=
(2013•朝阳区一模)已知:一次函数y=x+2与反比例函数y= (2013•朝阳区一模)如图,AB为⊙O的直径,BC是弦,OE⊥BC,垂足为F,且与⊙O相交于点E,连接CE、AE,延长OE到点D,使∠ODB=∠AEC.
(2013•朝阳区一模)如图,AB为⊙O的直径,BC是弦,OE⊥BC,垂足为F,且与⊙O相交于点E,连接CE、AE,延长OE到点D,使∠ODB=∠AEC. (2013•朝阳区一模)如图,抛物线y=-
(2013•朝阳区一模)如图,抛物线y=-