题目内容
【题目】如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连接BC,∠P=∠B. 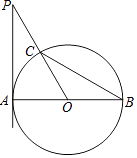
(1)求∠P的度数;
(2)连接PB,若⊙O的半径为a,写出求△PBC面积的思路. 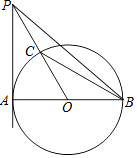
【答案】
(1)解:∵PA切⊙O于点A,
∴PA⊥AB,
∴∠P+∠POA=90°.
∵∠POA=∠B+∠OCB,
∴∠P+∠B+∠OCB=90°,
∵OB=OC,
∴∠B=∠OCB.
又∵∠P=∠B,
∴∠P=∠B=∠OCB.
∴∠P=30°;
(2)解:
∵在Rt△PAO中,∠APO=30°,OA=a,
∴PA= ![]() ,
,
∴△PBC面积是 ![]() PA×AB=
PA×AB= ![]() ×
× ![]() a×(a+a)=
a×(a+a)= ![]() a2
a2
【解析】(1)根据切线的性质求出∠PAB=90°,求出∠P=∠B=∠OCB,即可得出答案;(2)解直角三角形求出AP,根据三角形面积公式求出即可.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
相关题目