题目内容
如图,在△ABC中,BC=7cm,AC=24cm,AB=25cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分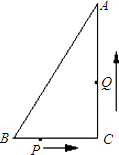 别从B、C同时运动,请解答下面的问题,并写出探索的主要过程:
别从B、C同时运动,请解答下面的问题,并写出探索的主要过程:(1)经过多少时间后,P、Q两点的距离为5
| 2 |
(2)经过多少时间后,S△PCQ的面积为15cm2?
(3)请用配方法说明,何时△PCQ的面积最大,最大面积是多少?
分析:(1)根据勾股定理PC2+CQ2=PQ2,便可求出经过1s后,P、Q两点的距离为5
cm2
(2)根据三角形的面积公式S△PCQ=
×PC×CQ便可求出经过2或1.5s后,S△PCQ的面积为15cm2
(3)根据三角形的面积公式S△PCQ=
×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大.
| 2 |
(2)根据三角形的面积公式S△PCQ=
| 1 |
| 2 |
(3)根据三角形的面积公式S△PCQ=
| 1 |
| 2 |
解答:解:(1)设经过ts后,P、Q两点的距离为5
cm,
ts后,PC=7-2t cm,CQ=5t cm,
根据勾股定理可知PC2+CQ2=PQ2,
代入数据(7-2t)2+(5t)2=(5
)2;
解得t=1或t=-
(不合题意舍去);
(2)设经过ts后,S△PCQ的面积为15cm2
ts后,PC=7-2t cm,CQ=5t cm,
S△PCQ=
×PC×CQ=
×(7-2t)×5t=15
解得t1=2,t2=1.5,
经过2或1.5s后,S△PCQ的面积为15cm2
(3)设经过ts后,△PCQ的面积最大,
ts后,PC=7-2t cm,CQ=5t cm,
S△PCQ=
×PC×CQ=
×(7-2t)×5t=
×(-2t2+7t)
当t=-
时,即t=
=1.75s时,△PCQ的面积最大,
即S△PCQ=
×PC×CQ=
×(7-2×1.75)×5×1.752=
当时间为1.75秒时,最大面积为
.
| 2 |
ts后,PC=7-2t cm,CQ=5t cm,
根据勾股定理可知PC2+CQ2=PQ2,
代入数据(7-2t)2+(5t)2=(5
| 2 |
解得t=1或t=-
| 1 |
| 29 |
(2)设经过ts后,S△PCQ的面积为15cm2
ts后,PC=7-2t cm,CQ=5t cm,
S△PCQ=
| 1 |
| 2 |
| 1 |
| 2 |
解得t1=2,t2=1.5,
经过2或1.5s后,S△PCQ的面积为15cm2
(3)设经过ts后,△PCQ的面积最大,
ts后,PC=7-2t cm,CQ=5t cm,
S△PCQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
当t=-
| b |
| 2a |
| 7 |
| 2×2 |
即S△PCQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 245 |
| 16 |
当时间为1.75秒时,最大面积为
| 245 |
| 16 |
点评:本题主要结合勾股定理和三角形面积公式的求法考查了二次函数的应用,是各地中考的热点,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B=
20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B= 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为 2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( )
2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( ) 如图,在△ABC中,AB=AC,且∠A=100°,∠B=
如图,在△ABC中,AB=AC,且∠A=100°,∠B=