题目内容
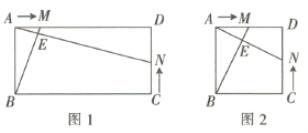
【题目】如图,在正方形![]() 中,
中,![]() ,点
,点![]() 在正方形边上沿
在正方形边上沿![]() 运动(含端点),连接
运动(含端点),连接![]() ,以
,以![]() 为边,在线段右侧作正方形
为边,在线段右侧作正方形![]() ,连接
,连接![]() 、
、![]() .
.
小颖根据学习函数的经验,在点![]() 运动过程中,对线段
运动过程中,对线段![]() 、
、![]() 、
、![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小颖的探究过程,请补充完整:
(1)对于点![]() 在
在![]() 、
、![]() 边上的不同位置,画图、测量,得到了线段
边上的不同位置,画图、测量,得到了线段![]() 、
、![]() 、
、![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 | 位置 | 位置 | 位置 | 位置 | 位置 | 位置 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
在![]() 、
、![]() 和
和![]() 的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数.
的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数.
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象:
中,画出(1)中所确定的函数的图象:
(3)结合函数图像,解决问题:
当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长约为
的长约为
【答案】(1)![]() ;(2)画图见解析;(3)
;(2)画图见解析;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)根据表格的数据,结合自变量与函数的定义,即可得到答案;
(2)根据列表、描点、连线,即可得到函数图像;
(3)可分为AE=DF,DF=DG,AE=DG,结合图像,即可得到答案.
解:(1)根据表格可知,![]() 从0开始,而且不断增大,则DG是自变量;
从0开始,而且不断增大,则DG是自变量;
![]() 和
和![]() 随着DG的变化而变化,则AE和DF都是DG的函数;
随着DG的变化而变化,则AE和DF都是DG的函数;
故答案为:![]() ,
,![]() ,
,![]() .
.
(2)函数图像,如图所示:
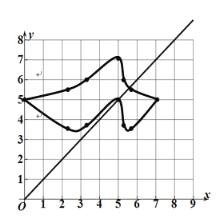
(3)∵![]() 为等腰三角形,则可分为:
为等腰三角形,则可分为:
AE=DF或DF=DG或AE=DG,三种情况;
根据表格和函数图像可知,
①当AE=DG=![]() 时,
时,![]() 为等腰三角形;
为等腰三角形;
②当AE=![]() 时,DF=DG=5.00,
时,DF=DG=5.00,![]() 为等腰三角形;
为等腰三角形;
③当AE=DF=![]() 时,
时,![]() 为等腰三角形;
为等腰三角形;
故答案为:![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目