题目内容
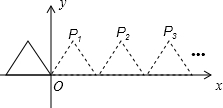 如图,将边长为2的等边三角形沿x轴正方向连续翻折2012次,依次得到点P1,P2,P3…P2012.则点P2012的坐标是
如图,将边长为2的等边三角形沿x轴正方向连续翻折2012次,依次得到点P1,P2,P3…P2012.则点P2012的坐标是(4023,
)
| 3 |
(4023,
)
.| 3 |
分析:根据等边三角形的性质易求得P1的坐标为(1,
);在等边三角形翻折的过程中,P点的纵坐标不变,而每翻折一次,横坐标增加2个单位(即等边三角形的边长),可根据这个规律求出点P2012的坐标.
| 3 |
解答:解:易得P1(1,
);
而P1P2=P2P3=2,∴P2(3,
),P3(5,
);
依此类推,Pn(1+2n-2,
),即Pn(2n-1,
);
当n=2012时,P2012(4023,
).
故答案为:(4023,
).
| 3 |
而P1P2=P2P3=2,∴P2(3,
| 3 |
| 3 |
依此类推,Pn(1+2n-2,
| 3 |
| 3 |
当n=2012时,P2012(4023,
| 3 |
故答案为:(4023,
| 3 |
点评:考查了规律型:点的坐标.解答此类规律型问题时,通常要根据简单的条件得到一般化规律,然后根据规律求特定的值.

练习册系列答案
相关题目
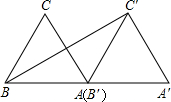 如图,将边长为3的等边△ABC沿着
如图,将边长为3的等边△ABC沿着| BA |
A、
| ||
B、2
| ||
C、3
| ||
D、4
|
 (2013•遵义)如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( )
(2013•遵义)如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( )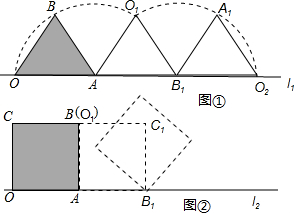
 如图,将边长为6cm的等边三角形△ABC沿BC方向向右平移后得△DEF,DE、AC相交于点G,若线段CF=4cm,则△GEC的周长是
如图,将边长为6cm的等边三角形△ABC沿BC方向向右平移后得△DEF,DE、AC相交于点G,若线段CF=4cm,则△GEC的周长是