题目内容
 如图,在等腰梯形△ABCD中,AB∥CD,AD=BC=CD,BD⊥AD.
如图,在等腰梯形△ABCD中,AB∥CD,AD=BC=CD,BD⊥AD.
(1)求∠A的度数.
(2)设AD=2cm,求梯形ABCD的面积.
(1)解:∵AD=BC=DC,
∴∠CDB=∠CBD,
∵DC∥BA,
∴∠CDB=∠DBA,
∴∠CBA=2∠DBA,
∵DC∥AB,AD=BC,
∴∠A=∠ABC=2∠DBA,
∵DB⊥AD,
∴∠ADB=90°,
∴∠A= ×90°=60°,
×90°=60°,
答:∠A=60°.
(2)解:作DE⊥AB于E,
∵∠A=60°,∠DEA=90°,
∴∠ADE=30°,
∴AE= AD=1cm,
AD=1cm,
由勾股定理得:DE= cm,
cm,
同理AB=2AC=4cm,
∴梯形ABCD的面积是 (CD+AB)×DE=
(CD+AB)×DE= ×(2cm+4cm)×
×(2cm+4cm)× cm=3
cm=3 cm2,
cm2,
答:梯形ABCD的面积是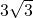 cm2.
cm2.
分析:(1)根据等腰三角形性质和平行线的性质推出∠CBA=∠A=2∠DBA,根据三角形的内角和定理求出即可;
(2)作DE⊥AB于E,求出∠DEA=∠DBA=30°,求出AE、AB、DE即可.
点评:本题主要考查对三角形的内角和定理,等腰三角形的性质,等腰梯形的性质,含30度角的直角三角形等知识点的理解和掌握,能正确运用性质进行推理和计算是解此题的关键.
∴∠CDB=∠CBD,
∵DC∥BA,
∴∠CDB=∠DBA,
∴∠CBA=2∠DBA,
∵DC∥AB,AD=BC,
∴∠A=∠ABC=2∠DBA,
∵DB⊥AD,
∴∠ADB=90°,
∴∠A=
 ×90°=60°,
×90°=60°,答:∠A=60°.

(2)解:作DE⊥AB于E,
∵∠A=60°,∠DEA=90°,
∴∠ADE=30°,
∴AE=
 AD=1cm,
AD=1cm,由勾股定理得:DE=
 cm,
cm,同理AB=2AC=4cm,
∴梯形ABCD的面积是
 (CD+AB)×DE=
(CD+AB)×DE= ×(2cm+4cm)×
×(2cm+4cm)× cm=3
cm=3 cm2,
cm2,答:梯形ABCD的面积是
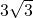 cm2.
cm2.分析:(1)根据等腰三角形性质和平行线的性质推出∠CBA=∠A=2∠DBA,根据三角形的内角和定理求出即可;
(2)作DE⊥AB于E,求出∠DEA=∠DBA=30°,求出AE、AB、DE即可.
点评:本题主要考查对三角形的内角和定理,等腰三角形的性质,等腰梯形的性质,含30度角的直角三角形等知识点的理解和掌握,能正确运用性质进行推理和计算是解此题的关键.

练习册系列答案
相关题目
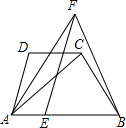 如图,在等腰梯形ABCD中,AB∥CD,AB=2CD,∠A=60°,又E是底边AB上一点,且FE=FB=AC,FA=AB.则AE:EB等于( )
如图,在等腰梯形ABCD中,AB∥CD,AB=2CD,∠A=60°,又E是底边AB上一点,且FE=FB=AC,FA=AB.则AE:EB等于( )| A、1:2 | B、1:3 | C、2:5 | D、3:10 |
 时运动停止.设运动时间为t秒.已知当t=
时运动停止.设运动时间为t秒.已知当t=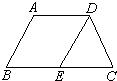 15、如图,在等腰梯形ABCD中,AB=2,AD=2,BC=4,DE∥AB,DE交BC于点E,则∠A的度数为
15、如图,在等腰梯形ABCD中,AB=2,AD=2,BC=4,DE∥AB,DE交BC于点E,则∠A的度数为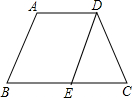 (1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
(1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
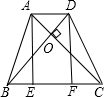 如图,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,AE⊥BC,DF⊥BC,垂足分别为E、F,设AD=2,BC=3,则四边形AEFD的周长是( )
如图,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,AE⊥BC,DF⊥BC,垂足分别为E、F,设AD=2,BC=3,则四边形AEFD的周长是( )