Question

如图，在等腰梯形ABCD中，AB∥DC，AD=BC=5cm，AB=12cm，CD=6cm，点Q从C开始沿CD边向D移动，速度是每秒1厘米，点P从A开始沿AB向B移动，速度是点Q速度的a倍，如果点P，Q分别从A，C同时出发，当其中一点到达终点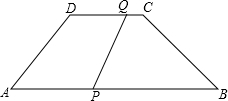时运动停止．设运动时间为t秒．已知当t=

3

2

时，四边形APQD是平行四边形．
（1）求a的值；
（2）线段PQ是否可能平分对角线BD？若能，求t的值，若不能，请说明理由；
（3）若在某一时刻点P恰好在DQ的垂直平分线上，求此时t的值．

Answer 1

分析：（1）利用平行四边形的性质，直接的出a的值；
（2）运用三角形的全等，得出△DOQ≌△BOP，即可得出DQ=BP，从而得出答案；
（3）过点C、D作CN⊥AB，DM⊥AB，交AB于点M、N，得出Rt△DAM≌Rt△CBN，再利用垂直平分线的性质以及矩形性质得出DM=NP，从而求出t．

解答：解：（1）∵四边形APQD是平行四边形
∴6-

3

2

=

3

2

a，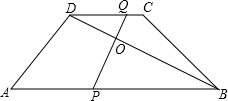
即：a=3；

（2）若线段PQ平分对角线BD，即DO=BO，
在△DOQ和△BOP中，
∵

∠QDO=∠OBP DO=OB ∠DOQ=∠POB

，
∴△DOQ≌△BOP（ASA）
∴DQ=BP
即：6-t=12-3t，
解得：t=3；

（3）分别过点C、D作CN⊥AB，DM⊥AB，交AB于点M、N
可得：四边形DMNC是矩形，
∴∠AMD=∠CNB=90°，AD=BC，DM=CN，
在Rt△DAM和Rt△CBN中
∵

AD=BC DM=CN

，
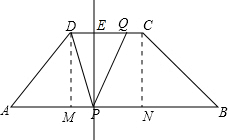
∴Rt△DAM≌Rt△CBN（HL），
∴AM=

12-6

2

=3
∵点P在DQ的垂直平分线EP上
∴PD=PQ，DE=

1

2

DQ，四边形DEPM是矩形
∴DE=PM，
即：

6-t

2

=3t-3，
解得：t=

12

7

．

点评：此题主要考查了平行四边形的性质，垂直平分线的性质和全等三角形的判定等知识，题目综合性较强，考查知识比较全面，证明线段相等经常运用证明三角形全等解决．