题目内容
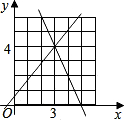 如图所示的是函数y=kx+b,y=mx+n的图象,
如图所示的是函数y=kx+b,y=mx+n的图象,(1)关于x、y的方程组
|
(2)若k<m,请根据图象确定k、b的值.
分析:(1)由于函数图象交点坐标为两函数解析式组成的方程组的解.因此联立两个函数解析式所得方程组的解,即为两函数图象的交点坐标.
(2)题可先根据两条直线斜率的大小关系,判定出y=kx+b所经过的点的坐标,然后用待定系数法求出k、b的值.
(2)题可先根据两条直线斜率的大小关系,判定出y=kx+b所经过的点的坐标,然后用待定系数法求出k、b的值.
解答:解:(1)关于x、y的方程组
的解是
;
(2)∵k<m,
∴图象经过点(3,4),(5,0)的直线为y=kx+b,得:
解得
.
则函数的解析式是y=-2x+10,
因而k=-2,b=10.
|
|
(2)∵k<m,
∴图象经过点(3,4),(5,0)的直线为y=kx+b,得:
|
|
则函数的解析式是y=-2x+10,
因而k=-2,b=10.
点评:在同一平面直角坐标系中,两个一次函数图象的交点坐标就是相应的二元一次方程组的解.反过来,以二元一次方程组的解为坐标的点,一定是相应的两个一次函数的图象的交点.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
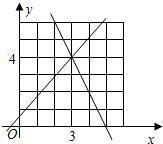 如图所示的是函数y=kx+b与y=mx+n的图象,求方程组
如图所示的是函数y=kx+b与y=mx+n的图象,求方程组 (2006•厦门模拟)下列几个函数图象可能如图所示的是函数( )
(2006•厦门模拟)下列几个函数图象可能如图所示的是函数( ) 如图所示的是函数y=kx+b与y=mx+n的图象,求方程组
如图所示的是函数y=kx+b与y=mx+n的图象,求方程组 如图所示的是函数y1=kx+b与y2=mx+n的图象,
如图所示的是函数y1=kx+b与y2=mx+n的图象,