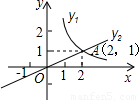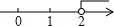题目内容
 如图所示的是函数y1=kx+b与y2=mx+n的图象,
如图所示的是函数y1=kx+b与y2=mx+n的图象,(1)方程
|
|
|
(2)y1中变量y1随x的增大而
减小
减小
;(3)在平面直角坐标系中,将点P(3,4)向下平移1个单位,恰好在正比例函数的图象上,求这个正比例函数的关系式.
分析:(1)从图象中找出两函数的交点坐标,即可得出方程组的解;
(2)根据图象和一次函数的性质即可得出y1中变量y1随x的增大而减小;
(3)设正比例函数的解析式为y=kx,求出平移后对应的点的坐标,代入求出k即可.
(2)根据图象和一次函数的性质即可得出y1中变量y1随x的增大而减小;
(3)设正比例函数的解析式为y=kx,求出平移后对应的点的坐标,代入求出k即可.
解答:解:(1)∵从图象可以得出两函数y1=kx+b与y2=mx+n的交点坐标是(3,4),
∴方程
的解是
;
(2)从图象可以看出:y1中变量y1随x的增大而减小,
故答案为:减小;
(3)设正比例函数的解析式为y=kx,
∵将点P(3,4)向下平移1个单位,恰好在正比例函数的图象上,
∴平移后对应的点的坐标是(3,3),
把(3,3)代入y=kx得:k=1,
∴正比例函数的解析式为y=x.
故答案为:
.
∴方程
|
|
(2)从图象可以看出:y1中变量y1随x的增大而减小,
故答案为:减小;
(3)设正比例函数的解析式为y=kx,
∵将点P(3,4)向下平移1个单位,恰好在正比例函数的图象上,
∴平移后对应的点的坐标是(3,3),
把(3,3)代入y=kx得:k=1,
∴正比例函数的解析式为y=x.
故答案为:
|
点评:本题考查了一次函数与二元一次方程组,一次函数的图象和性质等知识点的应用,主要考查学生运用知识点解决问题的能力,用了数形结合思想.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
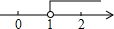
 14、如图所示,反比例函数y1与正比例函数y2的图象的一个交点坐标是A(2,1),若y2>y1>0,则x的取值范围在数轴上表示为( )
14、如图所示,反比例函数y1与正比例函数y2的图象的一个交点坐标是A(2,1),若y2>y1>0,则x的取值范围在数轴上表示为( ) 13、如图所示,正比例函数y1=kx与一次函数y2=-x+a的图象交于点A,根据图上给出的条件,回答下列问题:
13、如图所示,正比例函数y1=kx与一次函数y2=-x+a的图象交于点A,根据图上给出的条件,回答下列问题: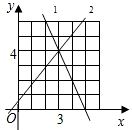 如图所示的是函数y1=kx+b与y2=mx+n的图象,
如图所示的是函数y1=kx+b与y2=mx+n的图象,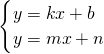 的解是________;
的解是________;