Question

【题目】已知：如图，点P是等边△ABC内一点，连接PC，以PC为边作等边三角形△PDC，连接PA，PB，BD．

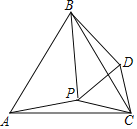
（1）求证：∠APC＝∠BDC；

（2）当∠APC＝150°时，试猜想△DPB的形状，并说明理由；

（3）当∠APB＝100°且DB＝PB，求∠APC的度数．

Answer 1

【答案】（1）见解析；（2）△DPB是直角三角形，理由见解析；（3）∠APC＝130°

【解析】

（1）由“SAS”可证△ACP≌△BCD，可得∠APC＝∠BDC；

（2）由全等三角形的性质可得∠BDC＝∠APC＝150°，∠PDC＝60°，可得∠BDP＝90°，即可求解；

（3）设∠APC＝x，由周角的性质和等边三角形的性质可得∠BPD＝200°﹣x，∠BDP＝x﹣60°，由等腰三角形的性质可列方程，即可求解．

（1）如图，∵△ABC，△PDC是等边三角形，

∴AC＝BC，PC＝PD＝CD，∠ACB＝∠PCD＝60°，

∴∠ACB-∠PCB＝∠PCD-∠PCB

∴∠ACP＝∠BCD，

∵AC＝BC，PC＝CD，

∴△ACP≌△BCD（SAS）

∴∠APC＝∠BDC；

（2）△DPB是直角三角形．

理由：∵∠BDC＝∠APC＝150°，∠PDC＝60°

∴∠BDP＝∠BDC﹣∠PDC＝90°，

∴△DPB是直角三角形；

（3）设∠APC＝x，则∠BPD＝=360°-100°-60°-x=200°﹣x，∠BDP＝x﹣60°

∵PB＝DB，

∴∠BPD＝∠BDP，

∴200°﹣x＝x﹣60°，

∴x＝130°，

∴∠APC＝130°