题目内容
如图,在某广场上空飘着一只气球P,A、B是地面上相距90米的两点,它们分别在气球的正西和正东,测得仰角∠PAB=45°,仰角∠PBA=30°,求气球P的高度(精确到0.1米)。

过点P作PC⊥AB于C,设PC = x米,
在Rt△PAC中,∠PAB=45°,
∴ AC =" PC" = x米,
在Rt△PBC中,∠PBA=30°,
∵ tan∠PBA =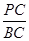 ,
,
∴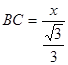 ,即
,即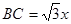 (米)
(米)
又∵ AB = 90米,
∴ AB =" AC" + CB = 米
米
∴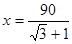 ≈32.9(米),
≈32.9(米),
答:气球P的高度约是32.9米。
在Rt△PAC中,∠PAB=45°,
∴ AC =" PC" = x米,
在Rt△PBC中,∠PBA=30°,
∵ tan∠PBA =
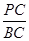 ,
,∴
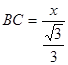 ,即
,即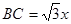 (米)
(米)又∵ AB = 90米,
∴ AB =" AC" + CB =
 米
米∴
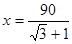 ≈32.9(米),
≈32.9(米),答:气球P的高度约是32.9米。
过点P作PC⊥AB于C点,由PC及∠A、∠B的正切值表示出AB,即AB=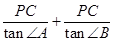 ,求得PC即可.
,求得PC即可.
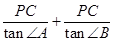 ,求得PC即可.
,求得PC即可.
练习册系列答案
相关题目
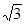 ≈1.7)
≈1.7)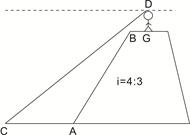
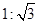 (即AB:BC=
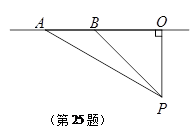
(即AB:BC=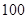 米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为
米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为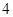 秒且∠APO=60°,∠BPO =45°.
秒且∠APO=60°,∠BPO =45°. 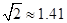 4,
4, 2).
2).
 ,堤高BC=5m,则坡面AB的长度是.
,堤高BC=5m,则坡面AB的长度是.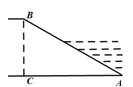
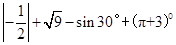 .
.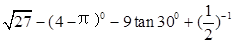
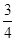 ,则BC的长是 。
,则BC的长是 。