题目内容
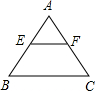 如图,一张边长为4的等边三角形纸片ABC,点E是边AB上的一个动点(不与A、B重合),EF∥BC交AC于点F.以EF为折痕对折纸片,当△AEF与四边形EBCF重叠部分的面积为
如图,一张边长为4的等边三角形纸片ABC,点E是边AB上的一个动点(不与A、B重合),EF∥BC交AC于点F.以EF为折痕对折纸片,当△AEF与四边形EBCF重叠部分的面积为| 3 |
分析:此题应分两种情况考虑:当折叠后△AEF的顶点A落在四边形BCFE内或BC边上时,重叠部分的面积即是三角形AEF的面积;当叠后△AEF的顶点A落在四边形BCFE外点A′处时,重叠部分的面积即是三角形AEF的面积减去A′MN的面积,根据轴对称的性质和相似三角形的性质进行计算.
解答: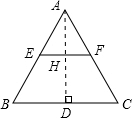 解:在等边△ABC中,作AD⊥BC于D,交EF于H,
解:在等边△ABC中,作AD⊥BC于D,交EF于H,
∴BD=DC=
BC=2.
又∵tan∠ABD=tan60°=
,
∴AD=2
;
∵EF∥BC,
∴△AEF∽△ABC.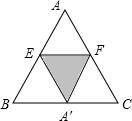
∴
=
,
=
.
∴AH=
EF,
∴S△AEF=
AH•EF.
S△AEF=
•
EF2=
EF2.
①当折叠后△AEF的顶点A落在四边形BCFE内或BC边上时,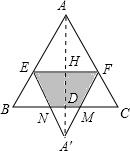
S△AEF=
EF2=
,
解得,EF=2;
②当折叠后△AEF的顶点A落在四边形BCFE外点A′处时,如图所示,A′F交BC于M,A′E交BC于N,连接AA′交EF于H,交BC于D.
∵
=
,
∴
=
,
又∵AH=A′H,
∴
=
,
∴
=
,
∴
=(
)2,
=
,
∴S△A′MN=
(2EF-4)2.
∴S四边形MFEN=
EF2-
(2EF-4)2=
,
解得,EF=
;
综上所述,EF的值是2或
.
故选D.
 解:在等边△ABC中,作AD⊥BC于D,交EF于H,
解:在等边△ABC中,作AD⊥BC于D,交EF于H,∴BD=DC=
| 1 |
| 2 |
又∵tan∠ABD=tan60°=
| AD |
| BD |
∴AD=2
| 3 |
∵EF∥BC,
∴△AEF∽△ABC.

∴
| AH |
| AD |
| EF |
| BC |
| AH | ||
2
|
| EF |
| 4 |
∴AH=
| ||
| 2 |
∴S△AEF=
| 1 |
| 2 |
S△AEF=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
①当折叠后△AEF的顶点A落在四边形BCFE内或BC边上时,

S△AEF=
| ||
| 4 |
| 3 |
解得,EF=2;
②当折叠后△AEF的顶点A落在四边形BCFE外点A′处时,如图所示,A′F交BC于M,A′E交BC于N,连接AA′交EF于H,交BC于D.
∵
| AH |
| AD |
| EF |
| 4 |
∴
| AH |
| HD |
| EF |
| 4-EF |
又∵AH=A′H,
∴
| A′H |
| HD |
| EF |
| 4-EF |
∴
| A′H |
| A′D |
| EF |
| 2EF-4 |
∴
| S△A′EF |
| S△A′MN |
| EF |
| 2EF-4 |
| ||||
| S△A′MN |
| EF2 |
| (2EF-4)2 |
∴S△A′MN=
| ||
| 4 |
∴S四边形MFEN=
| ||
| 4 |
| ||
| 4 |
| 3 |
解得,EF=
| 10 |
| 3 |
综上所述,EF的值是2或
| 10 |
| 3 |
故选D.
点评:本题考查的是翻折变换(折叠问题).此题采用了“分类讨论”的数学思想,以防漏解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
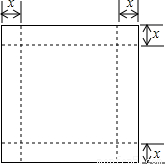
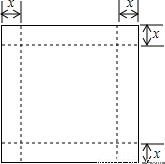
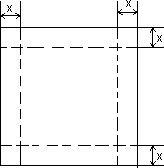 7、如图,一张边长为16cm的正方形硬纸板,把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
7、如图,一张边长为16cm的正方形硬纸板,把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为Vcm3,请回答下列问题: