题目内容
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.试探索以下问题:
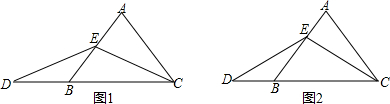
(1)当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE
(2)当点E为AB上任意一点时,如图2,AE与DB的大小关系会改变吗?请说明理由.
(3)在等边三角形ABC中,若点E在直线AB上,点D在直线BC上,且ED=EC,当△ABC的边长为1,AE=2时,CD的长为多少?

(1)当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE
=
=
DB(填“>”“<”或“=”).(2)当点E为AB上任意一点时,如图2,AE与DB的大小关系会改变吗?请说明理由.
(3)在等边三角形ABC中,若点E在直线AB上,点D在直线BC上,且ED=EC,当△ABC的边长为1,AE=2时,CD的长为多少?
分析:(1)根据等边三角形性质和等腰三角形的性质求出∠D=∠ECB=30°,求出∠DEB=30°,求出BD=BE即可;
(2)过E作EF∥BC交AC于F,求出等边三角形AEF,证△DEB和△ECF全等,求出BD=EF即可;
(3)当D在CB的延长线上,E在AB的延长线式时,由(2)求出CD=3,当E在BA的延长线上,D在BC的延长线上时,求出CD=1.
(2)过E作EF∥BC交AC于F,求出等边三角形AEF,证△DEB和△ECF全等,求出BD=EF即可;
(3)当D在CB的延长线上,E在AB的延长线式时,由(2)求出CD=3,当E在BA的延长线上,D在BC的延长线上时,求出CD=1.
解答:解:(1)如图1,∵△ABC是等边三角形,点E是AB的中点,
∴CE平分∠ACB,CE⊥AB,
∴∠ACB=60°,∠BEC=90°,AE=BE,
又∵ED=EC,
∴∠D=∠ECB=30°,
∴∠DEC=120°,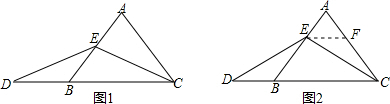
∴∠DEB=120°-90°=30°,
∴∠D=∠DEB=30°,
∴BD=BE=AE,即AE=DB.
故答案为:=.
(2)当点E为AB上任意一点时,如图2,AE与DB的大小关系不会改变.理由如下:
如图2,过E作EF∥BC交AC于F,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠A=60°,AB=AC=BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,即∠AEF=∠AFE=∠A=60°,
∴△AEF是等边三角形,
∴AE=EF=AF,
∵∠ABC=∠ACB=∠AFE=60°,
∴∠DBE=∠EFC=120°,∠D+∠BED=∠FCE+∠ECD=60°,
∵DE=EC,
∴∠D=∠ECD,
∴∠BED=∠ECF,
在△DEB和△ECF中,
,
∴△DEB≌△ECF(AAS),
∴BD=EF=AE,即AE=BD,
(3)解:CD=1或3,
理由是:分为两种情况: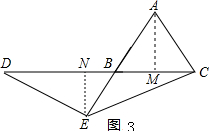
①如图3,过A作AM⊥BC于M,过E作EN⊥BC于N,
则AM∥EN,
∵△ABC是等边三角形,
∴AB=BC=AC=1,
∵AM⊥BC,
∴BM=CM=
BC=
,
∵DE=CE,EN⊥BC,
∴CD=2CN,
∵AM∥EN,
∴△AMB∽△ENB,
∴
=
,
∴
=
,
∴BN=
,
∴CN=1+
=
,
∴CD=2CN=3;
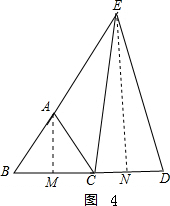
②如图4,作AM⊥BC于M,过E作EN⊥BC于N,
则AM∥EN,
∵△ABC是等边三角形,
∴AB=BC=AC=1,
∵AM⊥BC,
∴BM=CM=
BC=
,
∵DE=CE,EN⊥BC,
∴CD=2CN,
∵AM∥EN,
∴
=
,
∴
=
,
∴MN=1,
∴CN=1-
=
,
∴CD=2CN=1,
即CD=3或1.
∴CE平分∠ACB,CE⊥AB,
∴∠ACB=60°,∠BEC=90°,AE=BE,
又∵ED=EC,
∴∠D=∠ECB=30°,
∴∠DEC=120°,

∴∠DEB=120°-90°=30°,
∴∠D=∠DEB=30°,
∴BD=BE=AE,即AE=DB.
故答案为:=.
(2)当点E为AB上任意一点时,如图2,AE与DB的大小关系不会改变.理由如下:
如图2,过E作EF∥BC交AC于F,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠A=60°,AB=AC=BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,即∠AEF=∠AFE=∠A=60°,
∴△AEF是等边三角形,
∴AE=EF=AF,
∵∠ABC=∠ACB=∠AFE=60°,
∴∠DBE=∠EFC=120°,∠D+∠BED=∠FCE+∠ECD=60°,
∵DE=EC,
∴∠D=∠ECD,
∴∠BED=∠ECF,
在△DEB和△ECF中,
|
∴△DEB≌△ECF(AAS),
∴BD=EF=AE,即AE=BD,
(3)解:CD=1或3,
理由是:分为两种情况:

①如图3,过A作AM⊥BC于M,过E作EN⊥BC于N,
则AM∥EN,
∵△ABC是等边三角形,
∴AB=BC=AC=1,
∵AM⊥BC,
∴BM=CM=
| 1 |
| 2 |
| 1 |
| 2 |
∵DE=CE,EN⊥BC,
∴CD=2CN,
∵AM∥EN,
∴△AMB∽△ENB,
∴
| AB |
| BE |
| BM |
| BN |
∴
| 1 |
| 2-1 |
| 1 |
| 2 |
∴BN=
| 1 |
| 2 |
∴CN=1+
| 1 |
| 2 |
| 3 |
| 2 |
∴CD=2CN=3;

②如图4,作AM⊥BC于M,过E作EN⊥BC于N,
则AM∥EN,
∵△ABC是等边三角形,
∴AB=BC=AC=1,
∵AM⊥BC,
∴BM=CM=
| 1 |
| 2 |
| 1 |
| 2 |
∵DE=CE,EN⊥BC,
∴CD=2CN,
∵AM∥EN,
∴
| AB |
| AE |
| BM |
| MN |
∴
| 1 |
| 2 |
| ||
| MN |
∴MN=1,
∴CN=1-
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=2CN=1,
即CD=3或1.
点评:本题综合考查了等边三角形的性质和判定,等腰三角形的性质,全等三角形的性质和判定,三角形的外角性质等知识点的应用,解(2)小题的关键是构造全等的三角形后求出BD=EF,解(3)小题的关键是确定出有几种情况,求出每种情况的CD值,注意,不要漏解啊.

练习册系列答案
相关题目
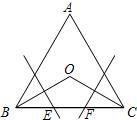 20、如图所示,在等边三角形ABC中,∠B、∠C的平分线交于点O,OB和OC的垂直平分线交BC于E、F,试用你所学的知识说明BE=EF=FC的道理.
20、如图所示,在等边三角形ABC中,∠B、∠C的平分线交于点O,OB和OC的垂直平分线交BC于E、F,试用你所学的知识说明BE=EF=FC的道理. 17、如图,已知在等边三角形ABC中,D、E是AB、AC上的点,且AD=CE.
17、如图,已知在等边三角形ABC中,D、E是AB、AC上的点,且AD=CE.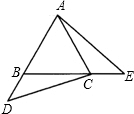 已知:如图,在等边三角形ABC中,点D、E分别是AB、BC延长线上的点,且BD=CE.
已知:如图,在等边三角形ABC中,点D、E分别是AB、BC延长线上的点,且BD=CE.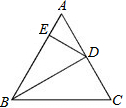 如图,在等边三角形ABC中,D为AC的中点,
如图,在等边三角形ABC中,D为AC的中点,