题目内容
 17、如图,已知在等边三角形ABC中,D、E是AB、AC上的点,且AD=CE.
17、如图,已知在等边三角形ABC中,D、E是AB、AC上的点,且AD=CE.求证:CD=BE.
分析:证CD=BE,应证明这两条线段所在的三角形全等.可利用SAS求证.
解答:证明:因△ABC是等边三角形,
所以BC=AC,∠A=∠ACB=60°.
在△ADC与△CEB中,
AC=BC,∠A=∠ACB,AD=CE,
所以△ADC≌△CEB.
故CD=BE.
所以BC=AC,∠A=∠ACB=60°.
在△ADC与△CEB中,
AC=BC,∠A=∠ACB,AD=CE,
所以△ADC≌△CEB.
故CD=BE.
点评:本题考查了全等三角形的判定与性质及等边三角形的性质;如果两条线段在两个三角形里,证明两条线段相等,通常情况下是证明这两条线段所在的两个三角形全等.

练习册系列答案
相关题目


 ,则等边三角
,则等边三角
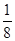 B.
B.  C.
C.
 D.1
D.1