题目内容
已知抛物线y=x2+2mx+n的顶点在直线y=-
x+
上,且过点(1,3),求这个抛物线的解析式.
| 1 |
| 2 |
| 1 |
| 2 |
考点:待定系数法求二次函数解析式
专题:
分析:把抛物线解析式写成顶点式形式,求出顶点坐标,然后代入直线解析式得到关于m、n的方程,再把点(1,3)代入抛物线解析式并用m表示出n,再联立两方程消掉n得到关于m的一元二次方程求解得到m,再求出相应的n值,最后写出抛物线的解析式即可.
解答:解:∵y=x2+2mx+n=(x+m)2-m2+n,
∴抛物线的顶点坐标为(-m,-m2+n),
∴-
×(-m)+
=-m2+n,
即2m2+m-2n+1=0①,
∵抛物线过点(1,3),
∴2m+n+1=3,
∴n=-2m+2②,
②代入①得,2m2+5m-3=0,
∴(2m-1)(m+3)=0,
∴2m-1=0,m+3=0,
解得m1=
,m2=-3,
当m1=
时,n=-2×
+2=1,
当m2=-3时,n=-2×(-3)+2=8,
∴抛物线的解析式为y=x2+x+1或y=x2-6x+8.
∴抛物线的顶点坐标为(-m,-m2+n),
∴-
| 1 |
| 2 |
| 1 |
| 2 |
即2m2+m-2n+1=0①,
∵抛物线过点(1,3),
∴2m+n+1=3,
∴n=-2m+2②,
②代入①得,2m2+5m-3=0,
∴(2m-1)(m+3)=0,
∴2m-1=0,m+3=0,
解得m1=
| 1 |
| 2 |
当m1=
| 1 |
| 2 |
| 1 |
| 2 |
当m2=-3时,n=-2×(-3)+2=8,
∴抛物线的解析式为y=x2+x+1或y=x2-6x+8.
点评:本题考查了待定系数法求二次函数解析式,一次函数图象上点的坐标特征,得到两个关于m、n的方程是解题的关键,也是本题的难点.

练习册系列答案
相关题目
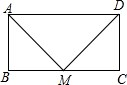 如图,在矩形ABCD中,M是BC的中点,过M作MA⊥MD,垂足为M,矩形的面积为128cm2,求矩形ABCD的周长.
如图,在矩形ABCD中,M是BC的中点,过M作MA⊥MD,垂足为M,矩形的面积为128cm2,求矩形ABCD的周长.