题目内容
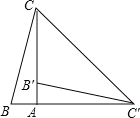
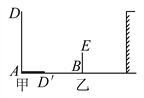
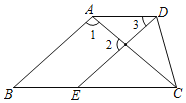
【题目】如图，∠1+∠2=180°，∠B=∠3，∠BCD=80°，求∠ADC的度数．
解：∵∠1+∠2=180°，（已知）
∴ ∥ ．（ ）
∴∠B=∠DEC．（ ）
∵∠B=∠3，（已知）
∴
∴AD∥BC，（ ）
∴ （两直线平行，同旁内角互补）
∵∠BCD=80°，
∴∠ADC= ．
【答案】AB∥DE；同旁内角互补，两直线平行；两直线平行，内错角相等；∠3=∠DEC；同位角相等，两直线平行；100°．
【解析】
根据平行线的判定得出AB∥DE，根据平行线的性质得出∠B=∠DEC，求出∠3=∠DEC，根据平行线的判定得出AD∥BC；根据平行线的性质得出∠ADC+∠BCD=180°，即可求出答案．
解：∵∠1+∠2=180°，（已知）
∴AB∥DE．（同旁内角互补，两直线平行）
∴∠B=∠DEC．（两直线平行，同位角相等）
∵∠B=∠3，（已知）
∴∠3=∠DEC
∴AD∥BC，（内错角相等，两直线平行）
∴∠ADC+∠BCD=180°，（两直线平行，同旁内角互补）
∵∠BCD=80°，∴∠ADC=100°．
故答案为：AB∥DE；同旁内角互补，两直线平行；两直线平行，内错角相等；∠3=∠DEC；同位角相等，两直线平行；100°．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】某商场设立了一个可以自由旋转的转盘，并规定：顾客购物10元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组落在奖品“铅笔”区域的统计数据：
转动转盘的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数 | 68 | 111 | 136 | 345 | 564 | 701 |
落在“铅笔”的成功率 |
（1）.计算并完成表格（精确到0.01）；
（2）.请估计，当
很大时，落在“铅笔”区域的频率将会接近______（精确到0.1）.
（3）.假如你去转动该转盘一次，你获得铅笔的成功率约是______.
