题目内容
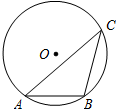
如图,AB是⊙O的直径,C是⊙O上一点,若AC:BC=4:3,AB=10,OD⊥BC于点D,则BD的长为( )

| A.1.5cm | B.3cm | C.5cm | D.6cm |

∵AB是⊙O的直径,
∴∠ACB=90°;
∵OD⊥BC,
∴AC∥OD,又∵AO=BO,
∴BD=CD;
设AC=4k,BC=3k;(k>0)
由勾股定理得:(4k)2+(3k)2=102,解得k=2;
∴BC=3k=6;
∴BD=CD=3cm.
故选B.
∴∠ACB=90°;
∵OD⊥BC,
∴AC∥OD,又∵AO=BO,
∴BD=CD;
设AC=4k,BC=3k;(k>0)
由勾股定理得:(4k)2+(3k)2=102,解得k=2;
∴BC=3k=6;
∴BD=CD=3cm.
故选B.

练习册系列答案
相关题目