题目内容
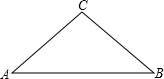如图，AB是等腰直角三角形的斜边，若点M在边AC上，点N在边BC上，沿直线MN将△MCN翻折，使点C落在AB上，设其落点为点P．当点P是边AB的中点时，求证：| PA |
| PB |
| CM |
| CN |
分析：根据折叠的性质可得MN∥AB，即可证明△CMN∽△CAB，即可得
=
=1=
，即可解题．
| CM |
| CN |
| AC |
| BC |
| PA |
| PB |
解答：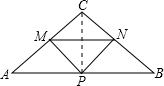
证明：连接PC，
折痕MN垂直PC，AC=BC，AP=BP．
由折叠可知MN⊥CP，
又∵△ABC为等腰三角形，P为AB的中点，
∴AB⊥CP，AP=PB，
∴
=1，MN∥AB，
∴△CMN∽△CAB．
∴
=
=1，
∴
=
．
证明：连接PC，折痕MN垂直PC，AC=BC，AP=BP．
由折叠可知MN⊥CP，
又∵△ABC为等腰三角形，P为AB的中点，
∴AB⊥CP，AP=PB，
∴
| PA |
| PB |
∴△CMN∽△CAB．
∴
| CM |
| CN |
| AC |
| BC |
∴
| PA |
| PB |
| CM |
| CN |
点评：本题考查了相似三角形的证明，相似三角形对应边比值相等的性质，本题中求证△CMN∽△CAB是解题的关键．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
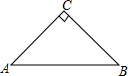
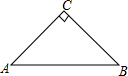如图，AB是等腰直角三角形ABC的斜边，若点M在边AC上，点N在边BC上，沿直线MN将△MCN翻折，使点C落在边AB上，设其落点为P．
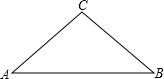如图，AB是等腰直角三角形的斜边，若点M在边AC上，点N在边BC上，沿直线MN将△MCN翻折，使点C落在AB上，设其落点为点P．当点P是边AB的中点时，求证：
．
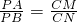如图，AB是等腰直角三角形ABC的斜边，若点M在边AC上，点N在边BC上，沿直线MN将△MCN翻折，使点C落在边AB上，设其落点为P．
=
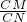成立吗？为什么？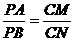
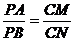是否仍然成立？请证明你的结论． 