题目内容
【题目】如图,△ABC中,AB=AC,BE⊥AC于E,且D、E分别是AB、AC的中点.延长BC至点F,使CF=CE.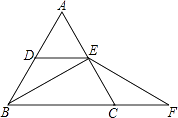
(1)求∠ABC的度数;
(2)求证:BE=FE;
(3)若AB=2,求△CEF的面积.
【答案】
(1)解:∵BE⊥AC于E,E是AC的中点,
∴△ABC是等腰三角形,即AB=BC,
∵AB=AC,
∴△ABC是等边三角形,
∴∠ABC=60°
(2)证明:∵CF=CE,
∴∠F=∠CEF,
∵∠ACB=60°=∠F+∠CEF,
∴∠F=30°,
∵△ABC是等边三角形,BE⊥AC,
∴∠EBC=30°,
∴∠F=∠EBC,
∴BE=EF
(3)解:过E点作EG⊥BC,如图:

∵BE⊥AC,∠EBC=30°,AB=BC=2,
∴BE= ![]() ,CE=1=CF,
,CE=1=CF,
在△BEC中,EG= ![]() ,
,
∴ ![]()
【解析】(1)根据等腰三角形的三线合一求出∠ABC的度数;(2)根据三角形的一个外角等于和它不相邻的两个内角的和、等腰三角形的性质得到BE=EF;(3)根据勾股定理求出BE的长,求出△CEF的面积.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目