题目内容
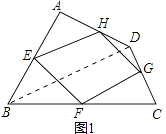
【题目】已知:如图1,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).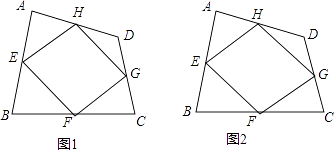
(1)四边形EFGH的形状是 , 证明你的结论.
(2)如图2,请连接四边形ABCD的对角线AC与BD,当AC与BD满足条件时,四边形EFGH是矩形;证明你的结论.
(3)你学过的哪种特殊四边形的中点四边形是矩形?说明理由.
【答案】
(1)平行四边形
(2)互相垂直
(3)
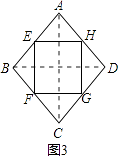
解:菱形的中点四边形是矩形.理由如下:
如图3,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,FG∥BD,EH= ![]() BD,FG=
BD,FG= ![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EH∥BD,HG∥AC,
∴EH⊥HG,
∴平行四边形EFGH是矩形.
故答案为:平行四边形;互相垂直.
【解析】解:(1)四边形EFGH的形状是平行四边形.理由如下:
如图1,连结BD.
∵E、H分别是AB、AD中点,
∴EH∥BD,EH= ![]() BD,
BD,
同理FG∥BD,FG= ![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
如图2,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;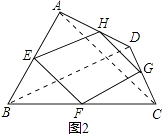
【考点精析】本题主要考查了矩形的判定方法的相关知识点,需要掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能正确解答此题.

 互动英语系列答案
互动英语系列答案