题目内容
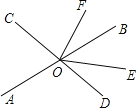
【题目】直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,垂足为O.
(1)若∠EOF=54°,求∠AOC的度数;
(2)①在∠AOD的内部作射线OG⊥OE;
②试探索∠AOG与∠EOF之间有怎样的关系?并说明理由.
【答案】(1)∠AOC=72°;(2)∠AOG=∠EOF
【解析】试题分析:(1)利用角平分线的性质结合已知得出∠DOE的度数,进而得出答案;
(2)①根据要求作图即可;
②由OG⊥OE得∠AOG+∠GOE+∠BOE=180°,由OF⊥CD得∠COF+∠FOE+∠DOE= 180°,又OE是角平分线,即可得出结论.
试题解析:(1)∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵∠EOF=54°,OD⊥OF,
∴∠DOE=36°,
∴∠BOE=36°,
∴∠AOC=72°;
(2)①如图所示,
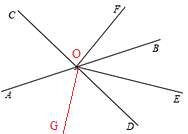
②∵OF⊥CD,
∴∠COF=90°,∠COF+∠EOF+∠EOD=180°,
∵OG⊥OE
∴∠GOE=90°,∠AOG+∠GOE+∠EOB=180°
∵OE平分∠BOD,
∴∠BOE=∠DOE,
∴∠AOG=∠EOF.

练习册系列答案
相关题目