题目内容
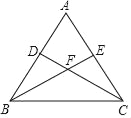
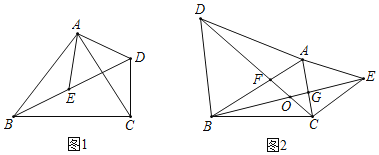
【题目】(1)问题发现:如图1,如果△ABC和△ADE均为等边三角形(等边三角形的三条边都相等,三个角都是60°),点B、E、D三点在同一直线上,连接CD.则CD与BE的数量关系为______;∠BDC的度数为______度.
(2)探究:如图2,若△ABC为三边互不相等的三角形,以它的边AB、AC为边分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,则CD与BE还相等吗?若相等,请证明,若不相等,说明理由:并请求出∠BOD的度数?
【答案】(1)相等,60;(2)CD=BE ;∠BOD=60°.
【解析】
(1)由条件△ABC和△ADE均为等边三角形,易证△ABE≌△ACD,从而得到对应边相等,即CD=BE;由△ABE≌△ACD,可得∠BEA=∠CDA,由点B,D,E在同一直线上,可求出∠BEA=120°,从而可以求出∠BDC的度数;
(2)根据等边三角形的性质和全等三角形的判定和性质得出CD=BE,∠ADC=∠ABE,进而解答即可.
(1)∵△ABC和△ADE均为等边三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=60°,
∴∠BAE=∠CAD.
在△ABE和△ACD中,
∵ ,
,
∴△ABE≌△ACD(SAS),
∴CD=BE,
∵△ABE≌△ACD,
∴∠BEA=∠CDA,
∵△AED为等边三角形,
∴∠AED=∠ADE=60°,
∵点B,D,E在同一直线上,
∴∠BEA=120°,
∴∠CDA=120°,
∴∠BDC=∠CDA-∠ADE=60°,
(2)∵以AB、AC为边分别向外做等边△ABD和等边△ACE,
∴AD=AB,AE=AC,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
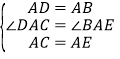 ,
,
∴△DAC≌△BAE(SAS)
∴CD=BE,∠ADC=∠ABE,
∵∠ABE+∠BFO+∠BOD=∠ADC+∠AFD+∠BAD=180°,
又∠BFO=∠AFD,∠ADC=∠ABE
∴∠BOD=∠BAD=60°.

 名校课堂系列答案
名校课堂系列答案