Question

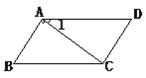
【题目】在△ABC 中，AB=AC，∠CAB=50°.在△ABC 的外侧作直线 AP，作 点 C 关于直线 AP 的对称点 D，连接 BD，CD，AD，其中 BD 交直线 AP 于点 E．

（1）如图 1，与 AD 相等的线段是_____；

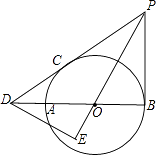
（2）如图 2，若∠PAC=20°，求∠BDC 的度数；

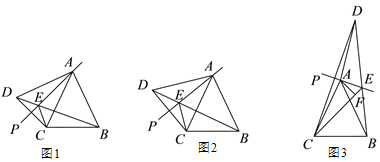
（3）如图 3，当 65°<∠PAC<130°时，作 AF⊥CE 于点 F，若 EF=1，BE=5，求 DE 的长．

Answer 1

【答案】（1）AC，AB；（2）25°；（3）7.

【解析】

(1)易得与 AD 相等的线段是 AC，AB；

（2）由点 C 与点 D 关于直线 AP 对称可得∠DAP=∠CAP=20°，∠DAC=40°∠ADC=70°，由（1）AD=AB,可得△ADB为等腰直角三角形，∠ADB=45°，可得∠BDC 的度数；

(3) 在 CE 上截取 GF=EF，连接 AG，点 C 与点 D 关于直线 AP 对称可得：AD=AC，∠ADE=∠ACE，可证的△ACG≌△ABE，得DE=CE=CG+2EF=BE+2EF=7.

（1）如图 1，与 AD 相等的线段是 AC，AB；

（2）∵点 C 与点 D 关于直线 AP 对称，

∴AD=AC，∠DAP=∠CAP=20°，

∴∠DAC=40°，∠ADC=70°又∠CAB=50°，

∴∠DAB=90°，

∵AC=AB，

∴AD=AB，

∴∠ADB=45°，

∴∠BDC=∠ADC-∠ADB=25°；

（3）在 CE 上截取 GF=EF，连接 AG，

∵点 C 与点 D 关于直线 AP 对称,

∴AD=AC，∠ADE=∠ACE，

∵AD=AC=AB，

∴∠ADB=∠ABD，

∴∠ACE=∠ABD，

∵AF⊥CE，GF=EF，

∴AG=AE，

∴∠AGE=∠AEB，

∵∠AED=∠AEG，

∴∠AGE=∠AED，

∴∠AGC=∠AEB

在△ACG 和△ABE 中，

ACG ABD，AGC AEB， AC AB，

∴△ACG≌△ABE（AAS），

∴BE=CG，

∵BE=5，CE=1，

∴DE=CE=CG+2EF=BE+2EF=7.