题目内容
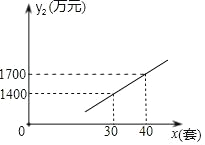
【题目】某商场经调研得出某种商品每天的利润y（元）与销售单价x（元）之间满足关系：y＝ax2+bx﹣75，其图象如图所示．
（1）求a与b的值；
（2）销售单价为多少元时，该种商品每天的销售利润最大？最大利润是多少元？（参考公式：当x＝
时，二次函数y＝ax2+bx+c（a≠0）有最小（大）值）
（3）销售单价定在多少时，该种商品每天的销售利润为21元？结合图象，直接写出销售单价定在什么范围时，该种商品每天的销售利润不低于21元？
【答案】（1）a=-1 ,b=20；(2)当x=10时，y值最大，最大值为25.即销售单价定为10元时，销售利润最大，为25元；(3)销售单价在8 ≤x ≤12时，销售利润不低于21元.
【解析】
（1）利用待定系数法求二次函数解析式得出即可；
（2）利用配方法求出二次函数最值即可；
（3）根据题意令y=21，解方程可得x的值，结合图象可知x的范围．
（1）y=ax2+bx-75图象过点（5，0）、（7，16），
∴
，
解得：
；
（2）∵y=-x2+20x-75=-（x-10）2+25，
∴当x=10时，y最大=25．
答：销售单价为10元时，该种商品每天的销售利润最大，最大利润为25元；
（3）根据题意，当y=21时，得：-x2+20x-75=21，
解得：x1=8，x2=12，
∴x=8或x=12即销售单价定在8元或12元时，该种商品每天的销售利润为21元；
故销售单价在8≤x≤12时，销售利润不低于21元．
练习册系列答案
阅读快车系列答案
相关题目
