题目内容
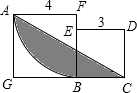
 如图,正方形BCDE和ABFG的边长分别为2a,a,连接CE和CG,则图中阴影部分的面积是
如图,正方形BCDE和ABFG的边长分别为2a,a,连接CE和CG,则图中阴影部分的面积是分析:(1)首先分别求出正方形ABFG、△AGC、△BEC的面积,利用S=S正方形ABFG+S△BCE-S△AGC,即可求出阴影部分的面积;
(2)利用勾股定理求出CE、CG的长比较即可.
(2)利用勾股定理求出CE、CG的长比较即可.
解答:解:(1)设图中阴影部分的面积是S,
则:S=S正方形ABFG+S△BCE-S△AGC,
∵S正方形ABFG=a×a=a2,
S△BCE=
•2a•2a=2a2,
S△AGC=
(a+2a)•a=
a2,
∴S=a2+2a2-
a2=
a2.
(2)在Rt△AGC和Rt△BEC中,由勾股定理得:
CE=
=
a,
CG=
=
a,
∴CE<CG.
故答案为:
a2,CE<CG.
则:S=S正方形ABFG+S△BCE-S△AGC,
∵S正方形ABFG=a×a=a2,
S△BCE=
| 1 |
| 2 |
S△AGC=
| 1 |
| 2 |
| 3 |
| 2 |
∴S=a2+2a2-
| 3 |
| 2 |
| 3 |
| 2 |
(2)在Rt△AGC和Rt△BEC中,由勾股定理得:
CE=
| (2a)2+(2a)2 |
| 8 |
CG=
| a2+(2a+a)2 |
| 10 |
∴CE<CG.
故答案为:
| 3 |
| 2 |
点评:本题主要考查了三角形的面积公式,面积和等积变换,勾股定理等知识点,找出S=S正方形ABFG+S△BCE-S△AGC是解此题的关键.

练习册系列答案
相关题目

 如图,扇形AFB恰为一个圆的
如图,扇形AFB恰为一个圆的
