题目内容
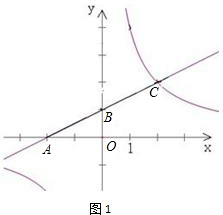
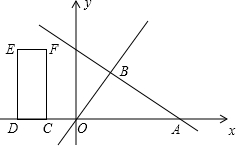
如图1,y=| 1 |
| 2 |
| k |
| x |
(1)求C点坐标及反比例函数解析式;
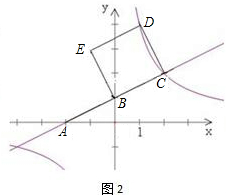
(2)如图2,D为反比例函数上一点,以CB,CD为边作平行四边形BCDE,问四边形BCDE能否是正方形?如果能,求出D点和另一顶点E的坐标;如果不存在,说明理由;
(3)如图3,过C点任作一直线,P为该直线上一点,满足∠BPE=135°,求证:PC-PE=
| 2 |

分析:(1)首先求出一次函数与坐标轴的交点坐标,进而求出C点的坐标,从而得出反比例函数的解析式;
(2)利用两点之间距离公式,求出BC的长进而得出CD的长,进而求出E点的坐标;
(3)利用三角形旋转的性质得出C,M,P三点共线,即PC-PE=PM=
BP.
(2)利用两点之间距离公式,求出BC的长进而得出CD的长,进而求出E点的坐标;
(3)利用三角形旋转的性质得出C,M,P三点共线,即PC-PE=PM=
| 2 |
解答:解:(1)∵y=
x+1交x轴于A,交y轴于B,
y=
x+1交x轴于A,
∴0=
x+1,
解得:x=-2,
A点的坐标为:(-2,0),
∵y=
x+1交y轴于B,
∴y=1,
∴B点的坐标为:(0,1),
∵C(m,m)是直线AB上一点,
∴m=
m+1,
解得:m=2,
C点的坐标为:(2,2),
∴反比例函数解析式为:y=
;
(2)∵C点的坐标为:(2,2),
B点的坐标为:(0,1),
∴BC=
,
当CD=
,
∴D点的坐标为:(1,4),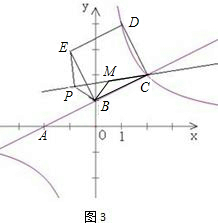
代入y=
,得出,(1,4)正好在函数图象上,
∴E点的坐标为:(-1,3);
(3)将△BPE绕点B顺时针旋转90°到△BMC,连接PM,
∵△BPM是等腰直角三角形,又∠BMC=135°,
∴C,M,P三点共线,
∴PC-PE=PM=
BP,
即PC-PE=
PB.
| 1 |
| 2 |
y=
| 1 |
| 2 |
∴0=
| 1 |
| 2 |
解得:x=-2,
A点的坐标为:(-2,0),
∵y=
| 1 |
| 2 |
∴y=1,
∴B点的坐标为:(0,1),
∵C(m,m)是直线AB上一点,

∴m=
| 1 |
| 2 |
解得:m=2,
C点的坐标为:(2,2),
∴反比例函数解析式为:y=
| 4 |
| x |
(2)∵C点的坐标为:(2,2),
B点的坐标为:(0,1),
∴BC=
| 5 |
当CD=
| 5 |
∴D点的坐标为:(1,4),

代入y=
| 4 |
| x |
∴E点的坐标为:(-1,3);
(3)将△BPE绕点B顺时针旋转90°到△BMC,连接PM,
∵△BPM是等腰直角三角形,又∠BMC=135°,
∴C,M,P三点共线,
∴PC-PE=PM=
| 2 |
即PC-PE=
| 2 |
点评:此题主要考查了反比例函数的综合应用,利用三角形相似求出对应边之间的大小关系进而得出CF=
PB是解决问题的关键.
| 2 |

练习册系列答案
相关题目
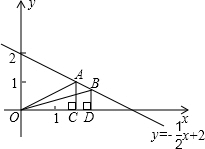 如图,一次函数y=-
如图,一次函数y=-| 1 |
| 2 |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、无法确定 |
 (1)求点B的坐标.
(1)求点B的坐标.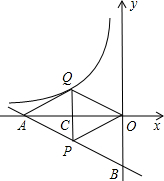 如图,一次函数y=-
如图,一次函数y=-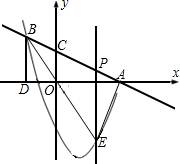 的交点是B,BD⊥x轴,垂足为D,且△ABD的面积是9.
的交点是B,BD⊥x轴,垂足为D,且△ABD的面积是9. 如图,直线
如图,直线